No Limitation
[논문 리뷰] Random Forest 본문

참고 강의
고려대학교 산업경영공학부 강필성 교수님
https://www.youtube.com/watch?v=nu_6PB1v3Xk
익히 알듯, RF는 bagging의 특수한 형태!
또한 RF의 경우 Decision Tree based의 알고리즘이라는 것을 기억하고 들어가자
Bagging의 경우는 데이터를 복원추출(Boostrap)해서 각 부스트랩마다 복잡도가 높은 모델들을 기본적으로 학습을 하는 포맷을 취하는데
Base Learner로는 인공 신경망, Decision Tree, Support Vector Machine들을 사용할 수 있다.
RF는 다음 2가지 방법을 통해 앙상블의 Diversity를 증가시키는데,
[1] Bagging
[2] Randomly chosen predictor variables
즉, 변수를 랜덤하게 선택한다는 것이다.
RF의 알고리즘을 한번 살펴보자

저기서도 트리를 구축할 때마다 p개의 변수 중 랜덤하게 m개를 선택한다고 나온다.
이러한 랜덤한 선택을 해주는 이유에 대해서는 뒤에서 살펴보자

가운데에 있는 것이 원 데이터라고 하면
왼쪽으로 boostrap해서 추출을 한 데이터는 학습 데이터
오른쪽 데이터는 Out Of Bag 데이터이다. [ Out of Bag에 대해서는 뒤에서 자세히 살펴볼 예정이다. ]
그렇다면 Randomly Selected는 어떠한 메커니즘으로 되는지 자세하게 살펴보자

본래는 이러한 25개의 피처로 구성된 데이터에서는 DT를 구축할 때 이러한 변수를 다 사용하게 된다.
하지만 RF의 경우는,
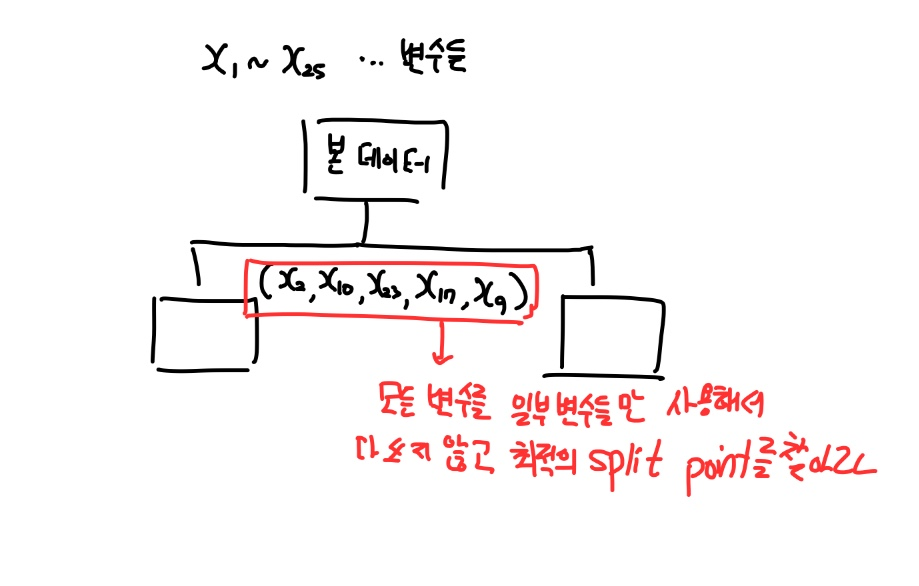
25개를 전부 사용하지 않고 본 데이터에 대해 일부 변수들만 사용해서 최적의 split을 찾게 한다.
이 것을 트리가 분할하면서 과정을 쭉 반복한다.
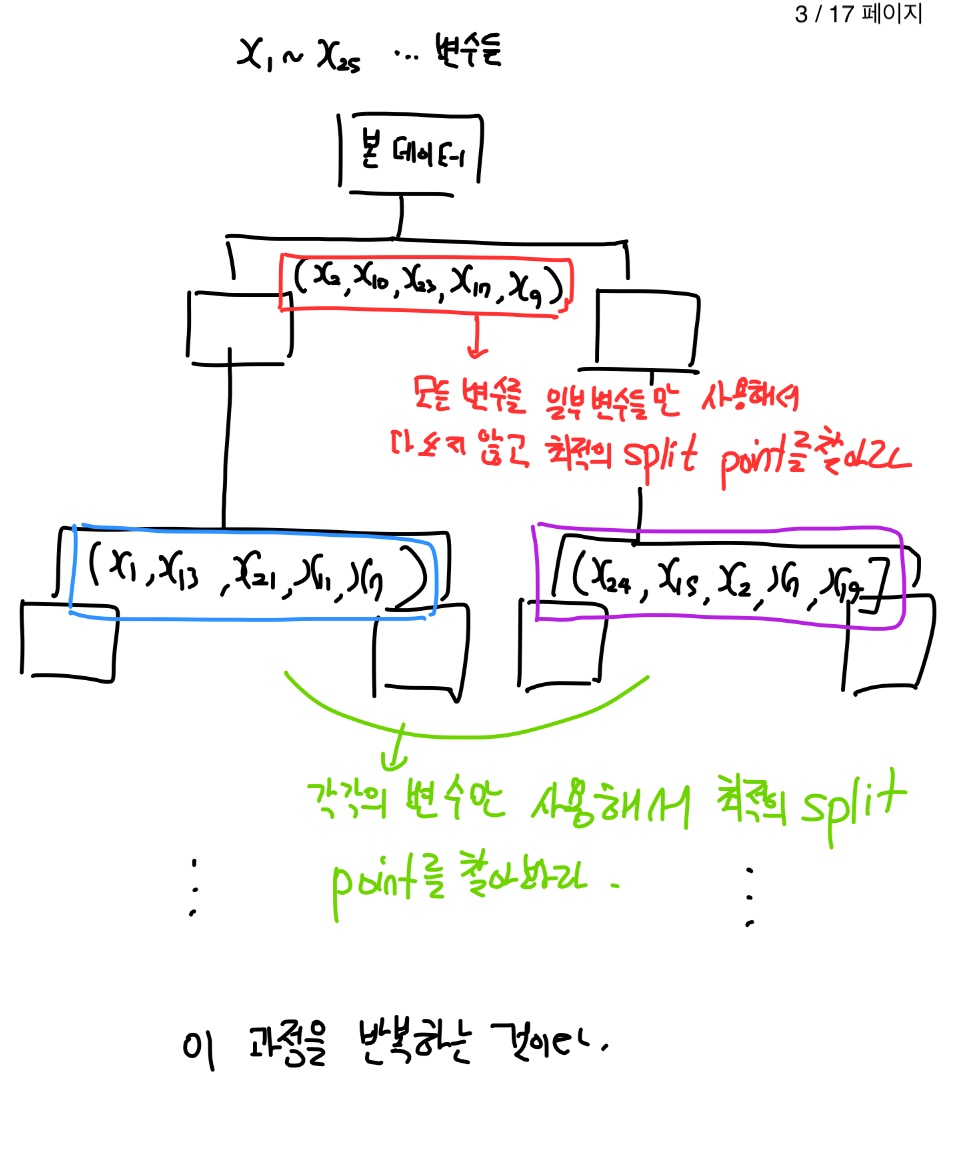
이렇게 진행을 하는 것이 어떠한 의미를 갖게 되는 것일까?
우선, Bagging 자체를 통해서 데이터의 "다양성"을 확보하게 된다.
다음으로, 모든 변수들을 각 트리에 다 사용하는 것이 Bagging Tree다.
하지만! 이러한 Bagging Tree는
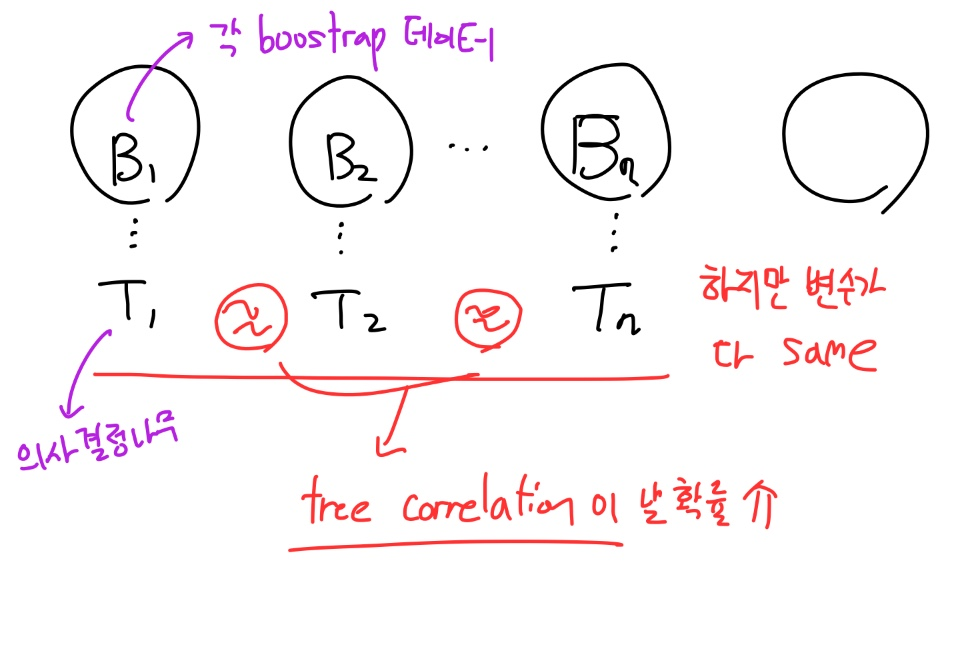
Tree correlation이 날 확률이 높다.
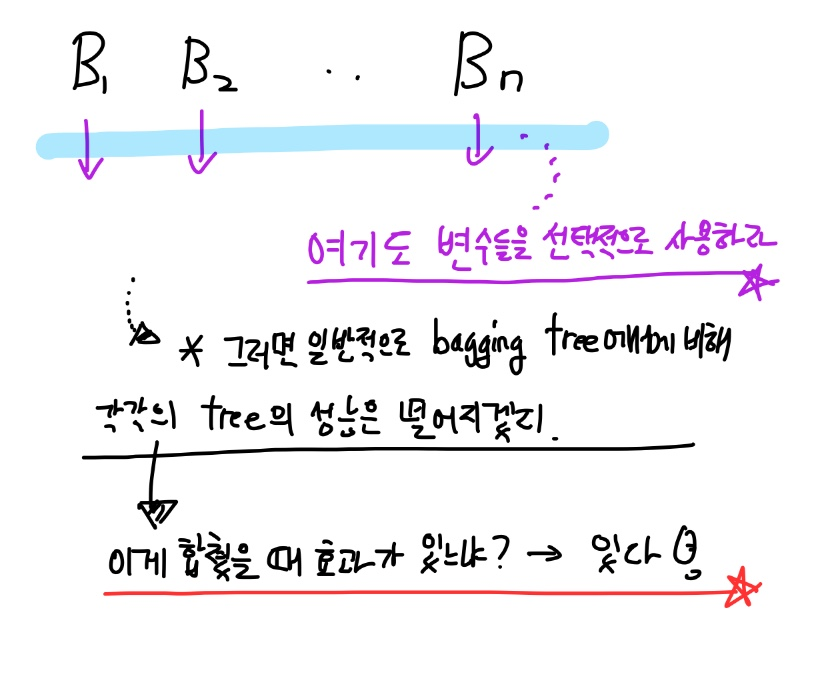
그렇다면 궁금한 점이 저 부분을 극복하기 위해 각 트리 별로 변수를 랜덤하게 뽑게 되면
모든 변수를 트리마다 다 사용한 bagging tree에 비해 각 트리의 성능이 떨어지게 되는데
이러한 트리들을 합쳤을 때 과연 효과가 있는 지의 여부인데, RF에서는 그 효과가 있음을 보이고 있다.
즉 변수 제한을 통해 다양성을 확보하게 되면 성능이 떨어지는 트리들의 결합이 전체 성능을 증가시킬 수 있는지를 체크하기 위해
다음 예시를 살펴보자

다음 케이스에서 A 군집은 B 군집에 비해 각 사람 별 평균 점수가 높다.
하지만 각 국영수를 한꺼번에 풀 때, 각 과목의 최고점을 선택하면
A : 국어 70 영어 80 수학 91
B : 국어 95 영어 95 수학 95 로 집단의 최고는 B가 더 높게 된다.
즉 이러한 경우처럼 각 평균의 성능은 떨어져도 최종 합친 결과가 더 높은 경우가 존재할 수 있다.
조금 더 구체적으로 "일반화 성능"을 살펴보자
각각의 트리들은 보다 다양성을 확보하기 위해 pruning을 하지 않고 데이터에 overfit을 시킨다.
그리고 개별 트리의 갯수가 충분히 크다면, 일반화 성능의 upper bound는 다음과 같이 설정할 수 있다.

위 수식에서

rho bar같은 경우, 각각의 개별적인 트리들이 가지고 있는 결과물들의 상관관계
( 다양성이 높을 수록 rho bar가 낮아짐 )

S 제곱의 경우 쉽게 말해 잘한 트리와 못한 트리의 격차를 보여주는 지표. 좋은 포레스트일수록 트리 간의 격차가 큼 → 즉 S 제곱이 큼 ( 잘할 수록 1에 가까워짐 )
위 수식의 경우 트리 간의 격차가 커지는 경우 줄어들고 트리 간의 상관성이 높을 수록 값이 커진다.
사례를 분석한 다음 슬라이드를 심층 공부하자!
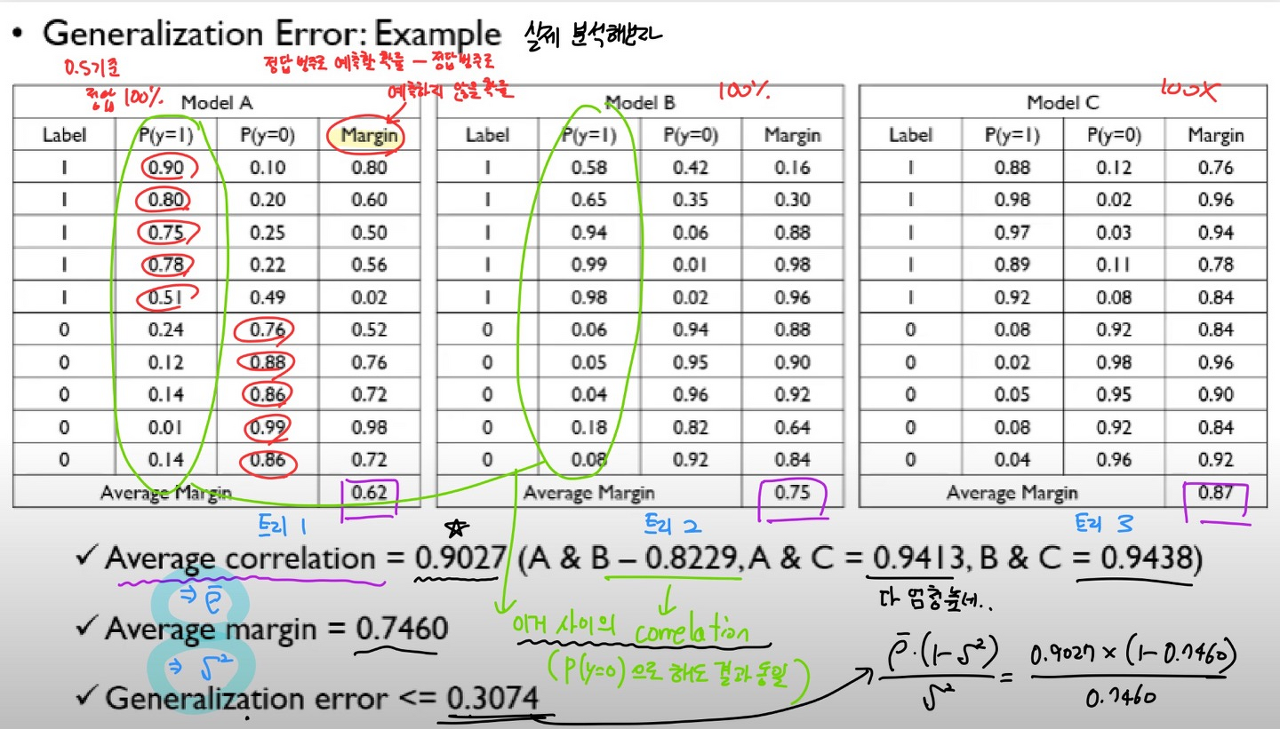
그렇다면 이러한 Generalization error가 의미하는 바는 무엇일까?
이렇게 완벽한 분류를 해내는 RF의 트리들 자체가 미래의 보이지 않는 테스트 에러에 대해서는 최대치로 가면 0.3074 정도의 에러가 날 것이다.
또한 RF의 중요한 특징은 바로 Feature Importance를 뽑을 수 있다
바로 Permutation 개념을 이용하여!
앞서 뽑아놓았던 OOB 데이터를 이용하여 Boostrap 데이터를 가지고 학습한 트리를 가지고 예측할 때 나오는 에러를 e라고 할 때, xi번째 변수의 중요도를 측정한다고 하면
pi는 xi번째 변수를 망치고 나서 예측할 때 나타나는 에러다.
여기서 (pi-ei)가 만약 차이가 거의 없게 되면 어떻게 될까?
: 이 말은 i번째 변수를 망쳐도 성능 감소가 별로 나타나지 않음을 의미하고 이는 곧 i번째 변수는 별로 중요한 변수가 아니라는 것을 알게 된다.
반면 (pi-ei)가 차이가 크게 되면?
: 이 말은 i 번째 변수가 중요함을 의미하게 된다.

즉, OOB Error 차이가 변수를 망쳤을 때 그 갭이 커야 하며 이는 모든 트리에서 나타나는 전반적인 특징 (편차가 적어야 하는 이유)이어야 변수가 중요하다고 판단할 수 있다.
그래서 (pi-ei)의 값을 di라고 하고
di의 표준편차를 나누어
vi = di/si를 구하게 되면
이 vi가 중요도 지수가 된다. → 단 이 vi의 절대적인 값 자체가 어떠한 의미를 갖는 것은 아님 (상대적인 중요도)
'논문 리뷰' 카테고리의 다른 글
| [논문 리뷰] Neural Machine Translation by Jointly Learning to Align and Translate (0) | 2022.02.04 |
|---|---|
| [논문 리뷰] Sequence to Sequence Learning with Neural Networks (0) | 2022.02.02 |
| [논문 리뷰] A Short Introduction to Boosting, Adaptive Boosting (0) | 2022.01.30 |
| [논문 리뷰] XGBoost : A Scalable Tree Boosting System (0) | 2022.01.29 |
| [논문 리뷰] LightGBM: A Highly Efficient Gradient Boosting Decision Tree (0) | 2022.01.29 |





