No Limitation
[Paper Review] Representation Learning with Contrastive Predictive Coding [개인공부용] 본문
[Paper Review] Representation Learning with Contrastive Predictive Coding [개인공부용]
yesungcho 2023. 11. 11. 17:07참 오랜만에 블로그 글을 올리는 것 같다.
개인 연구에서 CPC를 사용하고 있는데 개념적으로 알기만 하고 구체적인 깊은 내용을 다 숙지하지 못하다 보니 이참에 정리를 해보자.
다음 포스팅은 고려대학교 산업경영학과 김정희 님의 자료를 참고하였음.
또한 아래 블로그 포스팅들을 참고하였음.
https://junia3.github.io/blog/InfoNCEpaper
Abstract
초록의 본문을 살펴보면
"In this work, we propose a universal unsupervised learning approach to extract useful representations from high-dimensional data."
"The key insight of our model is to learn such representations by predicting the future in latent space by using powerful autoregressive models."
말이 어려운데, 결국 핵심은, 기존에 정답 label을 통해 neural network를 가이드해서 representation을 학습하는 방식이었다면, 그런 별도의 label 없이 자체적으로 "비교"를 통해 모형이 유사한 것 (관심 있는 것 등, positive sample)은 가깝게, 유사하지 않는 것 (관심 없는 것 등, negative sample)은 멀게 학습하는 방법을 통해 representation을 학습한다.
아래 이미지를 통해 쉽게 이해할 수 있다.
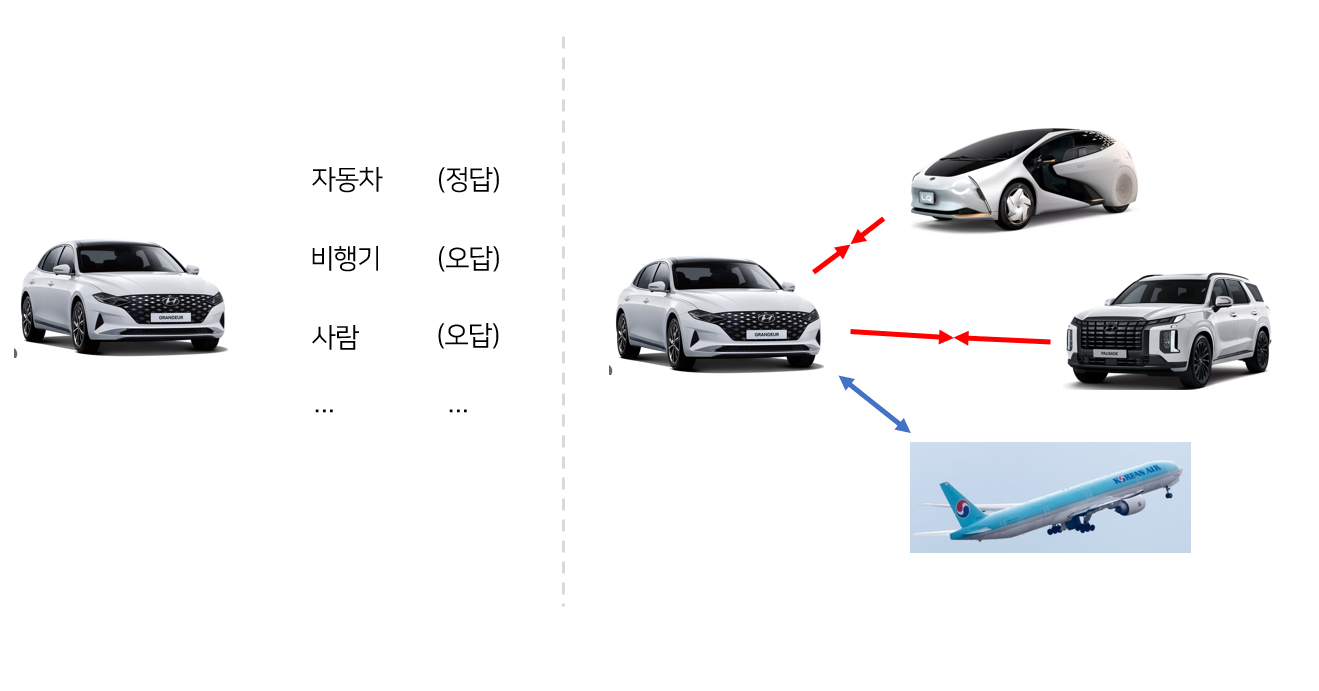
왼쪽의 경우는 정답 label이 주어져서 이를 바탕으로 모형을 학습하는 방법이고 우측의 경우는 "비교"를 수행하면서 학습을 수행하는 것을 의미한다. 이 비교를 수행하려면 결국 "유사성"을 정의할 필요가 있는데 이것은 어떻게 학습하는 걸까? 여기서는 "공유 정보 (Mutual Information)"라는 것을 바탕으로 유사성을 측정하고 "잡음 대비 추정 (Noise Contrastive Estimation)"이라는 기술을 사용하여 학습을 수행한다. 하나씩 살펴보자
Introduction
Supervised learning을 바탕으로 representation power를 키우는 것은 강력한 방법이다. 하지만 이 경우 특정 task에 over-specialized되는 문제가 있다. 이게 무슨 말이냐면, 예를 들어 image classification을 학습한 네트워크가 도출하는 feature는 상대적으로 그 task 대비 image captioning 같은 다른 task를 수행할 때 있어서는 상대적으로 유용한 정보가 부족하게 된다. 나아가, 이것이 다양한 modality, 즉 다양한 데이터 유형인 경우 (오디오, 음성, 자연어, 이미지 이런게 짬뽕되면) 더더욱 그 정보를 뽑아내기가 어려운 것이다. 그래서 특정 task 기반이 아닌 전반적으로 다양한 task를 수행함에 있어서 잘~ 뽑힌, 즉 representation power가 강력한 feature를 학습할 필요가 있다. 이를 위해서는 label에 의지하지 않는 unsupervised learning 방법이 많이 연구가 되어야 한다고 저자는 주장한다.
이를 위해 저자는 "Predictive Coding"이라는 개념을 가져온다.
Predictive Coding이란? 논문에는 다음과 같이 표기되어 있다.
"Predictive Coding is the one of the most common strategies for unsupervised learning, which has been to predict future, missing, or contextual information."
쉽게 얘기하면 미래를 예측하려고 하거나 문맥을 파악하려고 할 때, 인간의 뇌가 동작하는 방식을 의미한다. 신경과학에서는 다양한 레벨의 추상화를 통해 뇌가 무언가를 예측하려고 시도한다고 설명하고, 이러한 방식을 공학에서는 데이터 압축이나 신호 처리에서 많이 사용한다고 한다.
이건 사실 딥러닝에서는 언어 모델 개발 시 많이 사용되는 고전 기법이다. 예를 들어 neighboring words (target words)를 예측하는 task에서 많이 수행된다.
"원숭이 엉덩이는 색깔이 ___ " 여기서 빈칸에는 뭐가 들어갈까?
예를 들어 뭐 이런 task를 수행한다고 치면, 저기서 인간의 뇌가 동작하는 방식처럼 predictive coding이 이루어지는 것이다.
"We hypothesize that these approaches are fruitful partly because the context from which we predict related values are often conditionally dependent on the same shared high-level latent information. And by casting thise as a prediction problem, we automatically infer these features of interest to representation learning."
다음 문장을 번역하면 다음과 같다.
"우리는 이러한 접근법이 성과를 내는 이유 중 일부는 우리가 관련 값들을 예측할 때 사용하는 맥락이 종종 동일한 공유 고수준 잠재 정보에 조건적으로 의존하기 때문이라고 가설하고 있으며, 이것을 예측 문제로 제시함으로써 우리는 표현 학습의 흥미로운 특성을 자동으로 추론합니다.”
예시를 살펴보면

저기서 우리는 "원숭이 엉덩이는 색깔이" 라는 맥락을 통해 뒤에 정답인 "빨개"를 유추할 수 있다. 즉, 모형도 이 정답과 동일한 level의 latent 정보에 의존해서 저 정답을 유추하게 된다. 이 Predictive Coding이라는 과정을 통해 관심 있는 feature를 간접적으로 잘 뽑아내게 된다.
따라서 본 연구는 다음과 같은 과정을 거친다.
- First, we compress high-dimensional data into a much more compact latent embedding space in which conditional predictions are easier to model
즉, 쉽게 말해 "빨개"를 더 잘 예측할 수 있게 저 문장을 대표할 수 있는 compact한 latent space를 찾으려고 하는 시도 로 보인다.
- Secondly, we use powerful autoregressive models in this latent space to make predictions many steps in the future.
그리고 그 예측 모형으로서 다음 것을 예측하는 RNN, LSTM, GRU 같은 autoregressive model을 활용함.
- Finally, we rely on Noise-Contrastive Estimation for the loss function in similar ways that have been used for learning word embeddings in natural language models, allowing for the whole model
이건 구체적으로 어떻게 representation, 즉 “비교”를 통해 학습할 건지를 구체적으로 잡음 대비 추정 (Noise-Contrastive Estimationㅡ NCE) 을 어떻게 사용할 것인지에 대해 설명하는 부분인데 이 부분은 뒤에서 자세하게 풀 예정이다. (공유 정보이론을 사용하는 것이 핵심)
Contrastive Predictive Coding
이 논문에서 제시하는 핵심 알고리즘 CPC는 어떤 건지 살펴보자
Motivation and Intuitions
이 연구의 motivation이 참 재밌는데 아래 문장을 살펴보자
"The main intuition behind our model is to learn the representations that encode the underlying shared information between different parts of the (high-dimensional) signal."
즉, “고차원” 공간에 embedding된 정보를 학습하겠다가 핵심인거 같은데 대체 이 “고차원”이라는 건 무엇일까?
고려대 DSBA 연구실의 김정희 님의 ppt 자료에는 재밌는 예시가 있는데 한번 살펴보자.

“너 가만 안둬”라는 문장을 입력으로 받을 때 위 그림에서 밑에 있을 수록 low-level information, 위로 갈 수록 high-level information을 의미한다. 즉 저 문장 혹은 음성을 입력으로 받으면 그 신호 자체가 low-level이 되고, 점점 이 문장이 의미하는 것, 그 정보를 함축하는 것이 바로 high-level information이다. 저기서 slow varying, fast varying이라는 것은 high-level일수록 더 그 의미가 global 한 정보를 갖게 되는데 “너 가만 안둬”라는 문장이 진행될 때마다 그 특징이 천천히 변함을 의미한다.
"When predicting further in the future, the amount of shared information becomes much lower, and the model needs to infer more global structure. This slow features that span many time steps are often more interesting."
즉, 한마디로 low-level은 굉장히 noise, 잡음이 심한 반면 high-level은 더 global한 특징을 뽑고자 하는 것이다. 특별히 time-series task에서는 이것이 매우 중요한데 stage가 진행됨에 따라, 우리는 과거에 대한 정보가 점점 잊혀지면서 보다 global 한 정보에 보다 더 귀를 기울이게 된다.
그러면 이 high-level information을 예측해야 (찾아내야) 하는데 이것이 여간 쉬운 것이 아니다. 여기서 우리가 일반적으로 지도 학습의 classification, regression에 사용되는 Cross Entropy loss, Mean Squared Loss 같은 것은 high-level information을 찾아내는 데에 그다지 도움이 되지 않는다고 언급한다. 왜냐하면 상대적으로 입력 신호 대비 정답 신호가 갖는 정보의 양이 현저히 적기 때문이다. 예를 들면, 이미지는 수 천개의 픽셀 정보를 입력으로 받지만 high-level 정보 중의 class label의 경우 현저히 적은 양의 정보를 가지고 있기 때문에, 충분한 공유 정보를 형성하기 어렵게 된다.
입력 데이터를 x, context를 c라고 할 때, 아래 수식을 directly modeling하는 것은 효과적으로 x와 c 간의 shared information을 추출하기 어렵다.
$P(x|c)$
그래서 저자는 “compact distributed vector representation”을 encoding하기 위해, x와 c 간의 상호정보의존량 (Mutual Information) 이라는 개념을 정보 이론에서 따와, modeling할 타겟을 정의한다.
$I(x;c)=\sum_{x,c} p(x,c)\log \frac{p(x|c)}{p(x)}$
이 부분을 설명한 원문을 살펴보자
"When predicting future information we instead encode the target x (future) and context c (present) into a compact distributed vector representations (via non-linear learned mappings) in a way that maximally preserves the mutual information of the original signals x and c. By Maximizing the mutual information between the encoded representations (which is bounded by the MI between the input signals), we extract the underlying latent variables the inputs have in common."
그렇다면 도대체 저놈의 공유 정보라는 게 뭔지 아래 포스팅을 통해 공부해보자
Mutual Information이란?
이 부분은 bskyvision 님의 블로그 포스팅들을 참고하였다.
여길 이해하려면 먼저 “정보 이론”에 대한 간략한 개념 이해가 필요하다.
정보 이론의 핵심 가설은 “잘 발생하지 않는 사건은 자주 발생하는 사건보다 정보량이 많음”이다. 즉 매일 같이 자주 비가 오는 장마철에 그 날 또 비가 오는 사건은 정보량이 크지 않지만 갑자기 눈이 와버리면 이건 거의 발생하지 않는 사건이 발생한 거기 때문에 가지는 정보량이 크다.
즉, 발생할 확률 P가 낮을 수록 그 사건이 갖는 정보량은 커지는 습성을 기반으로 다음과 같은 수식으로 일반적으로 정보량을 정의한다.
어떤 사건 $x_{j}$에 대해 다음과 같이 정의할 수 있다.
$I(x_{j}) = -\log_{2} P(x_{j})$
밑은 2가 일반적으로 쓰이지만 어떤 정보인지에 따라 다르다고 한다.
그리고 저건 직관적으로 아래와 같은 형태의 함수를 갖기 때문에 P가 커질수록 I가 작아지는 형태를 띄게 된다.

그리고 이러한 정보량을 특정 j만 이 아니라 전반적인 정보량을 알고 싶을 때, “평균 정보량”을 계산하게 되는데 바로 이 “평균 정보량”이 흔히들 이야기하는 "엔트로피"가 된다.
$H(x) = -\sum_{j=1}^{n} p(x_{j})\log_{2} p(x_{j})$
이제 이 엔트로피를 바탕으로 다양한 사건들이 갖는 확률 변수들 사이의 정보량을 계산할 수 있다. 아래 벤다이어그램을 보면, 우리는 X, Y라는 확률 변수 2개에 대해서 다음과 같은 수식을 정의할 수 있는데, 각각 결합 엔트로피 H(X,Y), 조건부 엔트로피 H(X|Y) or H(Y|X), 그리고 공유 정보 I(X,Y) 로 구성되어 있다. 최종적으로 우리는 “공유 정보”라는 녀석을 뜯어볼 거다.

결합 엔트로피는 다음과 같이 정의된다.
$H(X,Y) = \sum_{x,y} p(x,y) \log_{2} \frac{1}{p(x,y)}$
조건부 엔트로피는 다음과 같이 정의된다. 이 때는 자명하게 교환법칙은 성립하지 않는다.
$H(Y|X) = \sum_{x} p_{X}(x)H(Y|X=x) = \sum_{x} p_{X}(x) \sum_{y} p_{Y|X}(y|x) \log_{2} \frac{1}{p_{Y|X}(y|x)}$
자 결국 우리가 알고 싶은 “공유 정보”는 어떻게 계산할까?
공유 정보란, “ 하나의 확률 변수가 다른 하나의 확률 변수에 대해 제공하는 정보의 양 ”을 의미한다. 이는 다른 의미로 “두 확률 변수가 공유하는 엔트로피”를 의미하기도 한다.
수식은 다음과 같다.
$I(X,Y) = \sum_{x,y} p(x,y)\log_{2} \frac{p(x,y)}{p(x)p(y)}$
그럼 본 연구에서는 어떻게 적용되나 보자.
우선 본 연구에서 세팅하는 autoregressive 모형의 구조에 대해 살펴보자. 여기는 음성 신호, 텍스트 신호를 기반으로 하기 때문에 RNN 계열을 기반으로 분석한다.

즉, 우리는 입력 $x_{t}$을 입력으로 받고 이를 통해 다음 시기의 $x_{t+1}$, $x_{t+2}$ 같은 미래를 예측하는 task를 수행하려고 한다. 이때 일반적인 autoregressive 모형은, encoder를 통해 latent vector $z_{t}$를 뽑아내고 이를 autoregression model을 통해 context vector $c_{t}$를 뽑아내는 일반적인 구조를 갖고 있다. 우리는 이 때, 직접적으로 $c_{t}$를 활용해서 $p_{k}(x_{t+k}|c_{t})$를 modeling을 하는 것이 아니라 $x_{t+k}, c_{t}$ 사이의 “공유 정보”를 모델링해서 그 공유정보를 최대화하는 방향으로 학습을 수행하고자 하는 것이다 (이게 아까 말한 "비교"라는 걸 의미한다.)
그래서 그 공유 정보 함수를 $f$라고 하면 이 $f$는 앞에서 언급한 공유 정보 값에 비례한 어떤 지표를 사용해야 함을 의미한다.
$f_{k}(x_{t+k}, c_{t}) \propto \frac{p(x_{t+k},c_{t})}{p(x_{t+k})p(c_{t})}$
이 때, 이 논문에서는 저 f를 사용하기 위해 “log-bilinear model”이라는 것을 사용한다.
그럼 저 녀석을 한번 간단히 뜯어보자.
Log-Bilinear Model이란?
두 벡터 사이의 관계를 파라미터화함으로써 공유 정보를 “학습”하게끔 유도하기 위해 본 연구는 Log-bilinear model을 사용한다. 여기서는 타겟이 되는 $X_{t+k}$에서 이를 encoder를 통과시킨 $Z_{t+k}$와 $C_{t}$ 사이의 두 벡터의 공유 정보를 계산한다. 두 벡터 $Z, C$가 있다고 가정해보자.
이 때 두 벡터 간의 공유 정보를 학습하기 위해서 아래와 같이 Z, C 사이의 가중치 W를 추가해서 파라미터화 시켜준다.
$Z_{t+k}^{T}W_{k}C_{t}$
이 수식을 일반적인 확률로 표현하기 위해 exponential 함수를 적용해주면 이 정보가 바로 벡터 $X$와 $C$ 가 갖는 “공유 정보”를 모델링 하는 함수가 된다.
$I(X_{t+k}^{T},C_{t}) = \exp(Z_{t+k}^{T}W_{k}C_{t})$
이 때 저 $W_k$는 step 마다 다른 가중치 매트릭스가 들어가게 된다. 예를 들어 아래 그림과 같이 $k$ 값에 따라 다른 $W_k$가 정의되는 것이다.
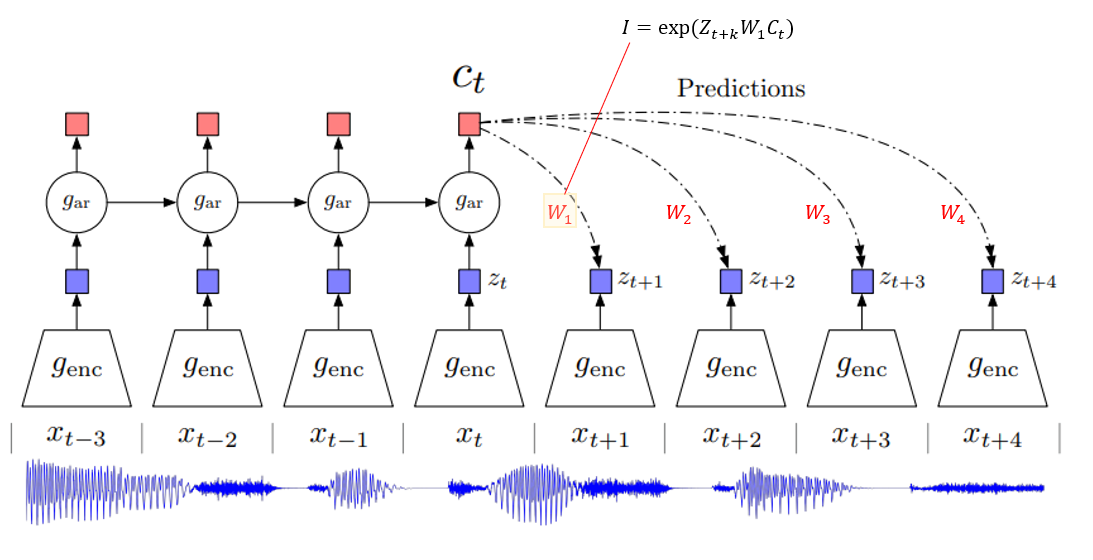
바로 이 공유 정보 $I$ 를 바탕으로 InfoNCE loss를 정의하는데, 그럼 여기서 InfoNCE loss를 들어가기 앞서, 사전 개념을 공부해야할 필요가 있다.
바로 InfoNCE Loss의 근간이 되는 NCE인데 이를 간단히 살펴보자
Noise Contrastive Estimation이란?
https://junia3.github.io/blog/InfoNCEpaper
이 부분은 JunYoung 님의 블로그 포스팅을 참고하였다.
우리가 NLP에서 다음과 같은 맥락 정보를 가지고 타겟을 예측하는 task를 수행할 때 다음 예시를 살펴보자

여기서 위에 “원숭이 엉덩이는 색깔이 _”를 예측할 때, 저기는 다양한 색깔과 관련된 단어들이 올 것인데 이걸 신경망 모형은 cross entropy loss를 통해 일반적으로 학습을 수행한다.
여기서 위 그림처럼 softmax 값을 구해서 정답인 “빨갛다”의 probability만 고려해서 backpropagation을 수행하게 된다. 그런데 이 때 $P(z_{i})$를 보면, 모든 위치의 단어에 대한 probability는 항상 같은 분모 (위 그림에서 초록색)를 가지게 된다. 바로 이 녀석 때문에 굳이 매번 parameter가 모든 training example에 대해 non-zero gradient term을 가진다고 한다. 그리고 이것이 바로 noisy한 학습을 유발한다고 설명한다. 극단적인 예로 저기에 “짜장면”이 들어갈 확률은 거의 없는데 그 embedding도 최적화하는 데에 사용되는 것은 학습에도 비효율적이고 메모리를 잡아먹는 것.
Negative Sampling
그래서 모든 voca를 고려하는 것이 아니라, 이 중에 일부, 즉 non-target word가 되는 녀석들을 뽑는 것인데 그것을 “Negative Samples”이라고 한다.
즉, 여기서는 embedding space 상에서, target word에 대한 확률 매핑을 추출하되, 전체 단어를 다 고려하지 않고 일부 추출된 negative sample과 target word인 positive sample을 고려해서 그 확률 매핑을 추출하게 된다.
NCE 논문은 logistic regression 모형을 상정하고 출발하는데, 우리 관심있는 target (positive sample)에 대한 분포를
$P$ (softmax를 통과한 확률 값으로 매핑), noise (negative samples)에 대한 분포를 $Q$라고 하면, log-odds를 다음과 같이 정의할 수 있다.
$logit = \log(\frac{P}{Q}) = \log(P)-\log(Q)$
바로 이 개념을 이제 InfoNCE Loss를 정의할 때 사용하는 것이다.
자 우리가 전체 데이터 $N$개가 있을 때 앞서 우리가 $c_{t}$를 가지고 미래 시점 $x_{t+k}$ 시점을 예측하고자 할 때, 이 $x_{t+k}$는 target (positive sample)이 되고, 나머지 $N-1$개의 $x$들은 전부 negative sample들이 된다. 이 때 우리는 다음과 같이 positive sample과 negative samples들이 가지는 분포, 나아가서 우리의 경우, positive sample과 negative samples들이 가지는 “공유 정보”에 대해서 다음과 같이 loss를 정의할 수 있다.
$\mathcal{L} = -E_{X}(\log\frac{P}{Q}) = -E_{X}(\log\frac{\exp(Z_{t+k}^{T}W_{k}C_{t})}{\sum_{j \neq k} \exp(Z_{t+j}^{T}W_{j}C_{t})})$
위 수식을 조금 더 쉽게 이해하면 다음과 같이 기술할 수 있다.

저기서 파란색 부분은 Mutual Information for Positive Pair가 되고 빨간색 부분이 Mutual Information for Negative Pair가 된다. 우리는 저 -를 제외하면 저 log term 내부를 최대화를 하고자 한다. 왜냐하면 positive sample과의 공유 정보를 최대화하고 negative samples들 과의 공유 정보를 최소화를 해야 target word를 잘 예측할 수 있기 때문이다. 반대로 -를 붙이게 되면 최소화를 하고자하게 되고 위 loss가 바로 InfoNCE Loss가 된다!
바로 이것이 우리가 익히 아는, “비슷한 것끼리는 유사하게 (positive pair), 다른 것 끼리는 멀게 (negative pairs)” 의 대조 학습의 근간을 이루게 된다.




