No Limitation
Knowledge distillation에서 projection-head의 역할 및 normalization의 중요성 본문
Knowledge distillation에서 projection-head의 역할 및 normalization의 중요성
yesungcho 2025. 5. 4. 17:47오늘은 많은 SSL 방법에도 사용되는 distillation 방법에서 기본적으로 많이 사용되는 projection-head의 구체적인 역할에 대한 수학적 고찰과 normalization이 어떤 역할을 하는 지에 대해 구체적으로 살펴보고자 합니다. 본 포스팅의 내용은 아래 논문의 내용을 정리하는 데에 목적이 있습니다. 하지만 실험 내용까지 디테일하게 다루지는 않고 개념적인 부분을 위주로 정리할 예정입니다. 또한 본 논문이 주장하는 바를 조금 더 critic하게 분석한 개인적인 견해는 이태릭체로 표시해 놓았으니 혹시 잘못됬거나 이상한 부분이 있으면 댓글로 남겨주시면 너무 감사할 것 같습니다.
Miles, R., & Mikolajczyk, K. (2024, March). Understanding the role of the projector in knowledge distillation. In Proceedings of the AAAI Conference on Artificial Intelligence (Vol. 38, No. 5, pp. 4233-4241).
https://ojs.aaai.org/index.php/AAAI/article/view/28219
본 논문에서는 우선 Knowledge Distillation에 사용되는 방법들 중 네트워크의 output space 직전의 feature embedding을 aligning하는 방법의 전략을 활용합니다. 이 외에, softmax 확률을 바탕으로 KL-divergence를 근사시키는 전통적인 방법부터 중간 중간에 있는 intermediate layer들을 통과시키는 feature를 근사시키는 방법들도 고려했으나 본 방법들은 아래와 같은 한계점이 있음을 지적합니다.
(1) softmax 기반 KL-divergence 근사 : Teacher network의 softmax prediction이 pseudo-label 처럼 활용될 수 있으나, 이는 downstream task가 classification이 아닌 경우에 확장성 측면에서 상대적으로 일반화되기 어려움이 있음을 지적하고, 또한 분류기가 distillation에 유용한 정보들을 collapse할 수 있음을 지적합니다. 즉, 가능하면 확률값이 아닌, feature embedding 값 그 자체를 활용하는 것에 주안점을 둔 것으로 판단됩니다. 아무래도 softmax prediction을 aligning하는 것보다 feature 자체를 aligning하는 것이 보다 fine-grained한 feature의 특징까지 distillation이 가능하기 때문에 그렇지 않을까 싶습니다.
(하지만 feature embedding 값 자체를 distillation하는 것에 비해 softmax 기반 근사가 더 좋은 점도 존재합니다. 예를 들어, feature aligning 방법은 너무 embedding 값 자체를 맞추느라 전체적인 데이터 분포와 맥락을 고려하지 않을 수 있습니다. 즉 collapse 문제에 빠질 우려도 존재합니다. 그리고 scale mismatch와 inductive bias 문제에 여전히 자유롭지 못하기 때문에 normalization과 non-linear projection-head가 잘 설계가 되어야 합니다.)
(2) Intermediate layer feature 근사 : 이 방법도 많이 사용되지만, 결국 teacher - student 간의 inductive bias가 다르면 제대로 distillation이 안 될 우려가 존재하고, 무엇보다 둘의 아키텍처가 아예 다르다면 어떤 부분의 layer의 feature를 사용할지도 어려운 문제가 존재합니다.
따라서, 본 논문은 맨 마지막 layer의 output space를 도출하기 직전의 feature embedding을 aligning의 target으로 활용합니다.
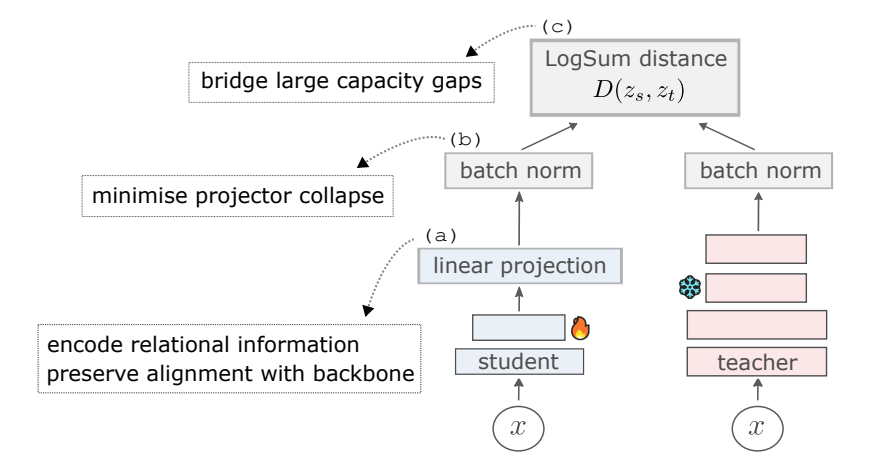
본 논문에서는 크게 3가지 포인트에서 분석이 들어가는데 첫 번째로는 (a) projection-head의 역할에 대해서 정리합니다. 그림에 보이는 것처럼 상대적 정보를 encoding한다고 하는데, 이게 무슨 말인지, 수식적으로는 어떤 정보들을 담고 있는 지를 디테일하게 들어가보고자 합니다. 두 번째로는 (b) batch normalization 의 중요성에 대해 언급합니다. 사실 이 부분은 꼭 batch norm이라기보다 normalization이 distillation에서 어떤 의미를 갖는 지를 디테일하게 다룹니다. 사실 논문에 언급은 없지만 다른 normalization (layer, group 등) 방법들도 충분히 확장 가능성이 있을 것으로 추측됩니다. 그리고 이 batch normalization을 넘어, 아예 whitening transformation의 개념도 적용이 가능할 부분으로 판단되어 이 부분을 수식적으로 디테일하게 다루고자 합니다. 그리고 마지막으로 (c) LogSum distance 는 단순히 L2 distance 같은 개념이 teacher와 student 간의 capacity gap이나 scale 차이가 큰 경우, loss가 안정적인 값이 나오지 않을 우려가 있기 때문에, 이런 경우 적합한 loss를 제안한다고 언급합니다.
그럼 하나씩 살펴보겠습니다.
본 논문에는 다음 문장이 있습니다.
"The projection weights encode relational information from previous samples"
저기서 projection head의 가중치는 과거 샘플들과의 상대적 정보를 encoding한다고 합니다. 과거 샘플들과의 정보를 encoding한다는 말의 의미는 무엇인지 살펴보겠습니다.
다음 그림을 살펴보겠습니다.

여기서 우리는 L2 loss를 가정하겠습니다. 위에 있는 L2 loss 수식에서 $Z_{s}$ 는 student feature를 의미하고 $Z_{t}$는 teacher feature를 의미합니다. 위 (1), (2) 는 몇 번째 배치의 입력인지를 나타내고 $W_{p}$는 projection head의 가중치를 의미합니다. 여기서 $W_{p}$는 학습이 되는 존재이므로 가변적이기 때문에 빨간색으로 표시했습니다.
위 아래 수식에서 첫 번째 발생한 loss로 인해 $W_{p}$는 업데이트 됩니다. 그리고 $W_{p}$는 첫 번째 배치의 정보를 학습한 상태입니다. 그리고 2번째 배치가 들어왔을 때, $W_{p}$는 두 번째 배치의 정보로 인해 업데이트가 됩니다. 이 때 $W_{p}$는 이미 첫 번째 배치를 학습했기 때문에 이미 첫 번째 배치를 알고 있는 상태입니다. 이 때 저자는 projection-head가 내재적으로 과거 배치와 현재 배치 간의 관계적인 정보 (relational information) 를 encoding한다고 언급합니다. 즉, 이는 많은 데이터에 학습을 하면 할수록 projection-head는 전반적인 데이터에 있는 관계적 정보를 고려해서 student의 특성을 teacher로 자동으로 transfer를 수행함을 의미합니다. 즉 무조건 특정 이미지 하나의 feature를 "똑같이 모방"하는게 아니라 (애초에 모든 이미지의 MSE loss가 0으로 수렴되게 할 수가 없음), 수 많은 입력 데이터가 들어가면서 "전반적인 경향"을 모방하도록 학습이 됨을 의미합니다. 어떻게 보면 cross-entropy minimization이 하려고 하는 것을 자체적으로 수행하는 것이기 때문에 저자는 별도로 softmax나 cosine similarity 같은 걸 계산하지 않아도 자체적으로 feature-aligning이 이런 역할들을 수행할 수 있다는 것을 언급합니다.
( 음 하지만, 조금 더 critic하게 생각해보면, 저 feature-aligning loss를 최대한 감소시키는 것을 목적으로 해서 구체적인 feature를 따라가지 않고 general한 경향을 따라간다고 했지만, 반면 distillation이 쉽게 되는 샘플들이 있고 어려운 샘플들이 있다고 하면 쉬운 샘플들만 잘 distillation하고 어려운 애들은 잘 안되는 collapse 문제가 존재할 가능성이 있다고 추측됩니다. 예를 들어 A와 B의 feature가 있을 때 loss를 줄이기 위해 A와 B 사이의 어떤 interpolated된 feature를 만들면 A와 B에서 loss가 각각 줄어드는 장점이 있습니다. 하지만, A와 B 둘 다 이 interpolated 된 feature는 실제 유사한 feature가 아니기 때문에 collapse 문제가 발생할 수 있다는 것입니다. 물론 이 부분을 보완하기 위해 본 논문은 LogSum loss에서 alpha 값을 4로 주어, 더 loss가 큰 애들이 극명하게 커지도록 하고 작은 애들을 더 작게 해, outlier에 민감하도록 설계하였지만, 본질적인 문제에서는 자유롭지 못할 것으로 추측됩니다 )
자 그렇다면 이 projection head를 사용해서 distillation을 수행하기 위해 loss를 바탕으로 gradient를 구해보면 다음과 같습니다.

우선 L2 loss를 바탕으로 계산한다고 했을 때 밑의 $W_{p}$에 대한 gradient를 계산한다고 하면, 다음과 같이 $C_{s}$와 $C_{st}$ 에 대한 항으로 나오게 됩니다. 이 때 $C_{s}$는 student feature의 self-correlation 정보를 담고 있고 $C_{st}$의 경우 student feature와 teacher feature의 cross correlation 정보를 반영하게 됩니다. 조금 더 깊게 들어가면, $C_{st}$는 student와 teacher 간의 상관성을 보여주는 matrix로서 teacher와 student 사이의 alignment 품질을 측정하게 되고, 이 품질의 정도에 따라 더 좋은 alignment matrix를 만들기 위해 $W_{p}$가 업데이트 됩니다. 반면, $C_{s}$는 최대한 feature 간의 redundancy가 적게끔하고, dominant한 feature에 쏠리지 않기 위해 최대한 Identity matrix 형태에 근사할수록 좋은 matrix가 됩니다. 이는 feature 간의 상관성을 갖지 않게끔 하는 것인데 만약 $C_{s}$ 에서 feature간의 상관성이 높게 되면, $C_{s}$의 다른 몇몇 dimension에만 정보가 몰리고 (collapse) 나머지는 zero-variance를 갖기 때문에 distillation 과정에서 relational 정보를 손실할 우려가 있습니다. 즉, $C_{s}$ 행렬은 선형 종속이 될 우려가 있고, 이는 정보 손실의 가능성이 있게 됩니다. 따라서, 만약 $C_{s}$가 단위 행렬 $I$가 된다면, 자기 자신을 제외하고 모든 dimension에 대해서는 상관성이 0이 되기 때문에, 위와 같은 collapse 문제에 자유롭게 됩니다. 이를 위해 가장 극단적으로 할 수 있는 가장 좋은 방법은 바로 Whitening Transformation 입니다.
본 논문에서는 다음과 같이 $C_{s}$가 $I$가 되는 경우를 언급하고 있습니다. 이 때 $W_{p}$의 gradient 수식은 아래와 같이 됩니다.

즉, $W_{p}$는 $C_{st}$가 되는 것입니다. 이는 Projection-head가 teacher와 student 사이의 alignment 자체를 수행하게 되는 것입니다.
자 그렇다면 이 Whitening Transformation은 어떻게 수행될까요? $C_{s}$가 $Z_{s}$의 Covariance를 의미할 때 우리는 다음을 찾는 것을 목적으로 합니다.

즉 $C_{s} = I$가 되게하는 $\tilde{Z_{s}}$ 를 찾는 것입니다.
우선 Whitening은 평균은 0, 분산은 1이 되게 하는 것이 목적입니다. 이 때, 분산이 각 dimension 마다 1이어야 하므로 Covariance matrix는 Identity Matrix가 되어야 합니다.
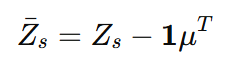


여기서 $\bar{Z_{s}}$ 는 zero-mean이 된 feature 이고 이의 분산을 계산해서 Idendity가 되게끔 하는 것이 목적입니다.
이 때 Transform Matrix를 $W$라고 할 때, 우리는 아래와 같이 전개할 수 있습니다.


다음처럼 $\tilde{Z_{s}}$ 의 Cov가 $I$가 되어야 합니다. 이를 만족하는 W를 찾아야 하므로 이를 다시 수식을 전개하면 아래와 같이 나오게 되고, 결국 $W$는 $\Sigma_{s}$의 inverse square root 형태여야 합니다.

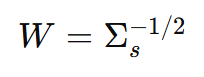
그리고 이는 $\Sigma_{s}$ matrix를 SVD 해서 eigenvalue의 inverse square root를 적용해서 $W$를 계산할 수 있습니다.


따라서 최종 $\tilde{Z_{s}}$는 아래와 같은 형태가 됩니다.
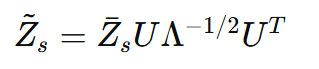
즉, Z 값이 $C_{s}$의 Covaraince가 Identity가 되게 하고, 이를 적용했을 때 feature decorrelation이 보장되게 됩니다.
하지만 왜 본 논문에서는 whitening transformation을 바로 적용하기 보다 batch normalization을 적용하는 걸까요? 그리고 이러한 효과는 batch normalization과 어떠한 연관이 있는 것일까요?
우선 Whitening Transformation은 수식에서 보다시피 feature의 dimension이 크게 되면 행렬의 사이즈가 커져 느려지는 단점이 있고 batch 가 적으면 $m$ 값이 작아져 학습이 보다 불안정해지는 단점이 있습니다. 그래서 이를 바로 사용하지 않고 본 효과를 어느 정도 커버할 수 있는 방법이 있는 지를 고민했습니다.
이 때 저자는 이러한 batch normalization을 whitening transformation을 대체해서 사용합니다. 본질적으로 완전히 whitening transformation이 수행하는 바를 대체하지는 못하지만 어느 정도 값이 쏠리는 문제는 막을 수 있음을 언급합니다.
Batch Normalization의 process를 다시 수식으로 살펴보겠습니다. 여기서 주의해야할 것은, 우리가 일반적으로 아는 BN에서 affine transformation은 적용하지 않고 그냥 평균과 분산을 활용한 normalization을 수행합니다. 왜냐하면 affine transformation을 적용하는 경우 평균이 0, 분산이 1인 보장이 깨지게 되어 whitening transformation의 효과가 약화되어 singular value collapse할 확률이 증가하게 됩니다. 우리는 표현력 자체를 상향시키는 것이 목적이 아닌, feature decorrelation이 목적이기 때문에 affine transformation은 제거하였습니다.
기본적인 batch normalization의 수식 형태는 아래와 같습니다.
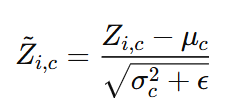
여기서 $Z_{s}$를 편의상 Z라고 쓰고 수식을 전개하겠습니다.




최종적으로 $\tilde{Z}$가 batch normalized된 feature라고 할 때 우리는 평균을 0으로 만들고, 분산을 1로 만드는 과정을 적용합니다. 이 때, $D$는 각 dimension 별로 분산 값을 나누는 형태의 연산을 $D^{-1}$ 을 곱하는 형태로 표현할 수 있습니다.
이 때 이 batch normalized 하기 전의 공분산 $Cov(Z)$와 적용 후 $Cov(\tilde{Z})$의 공분산은 아래와 같습니다.
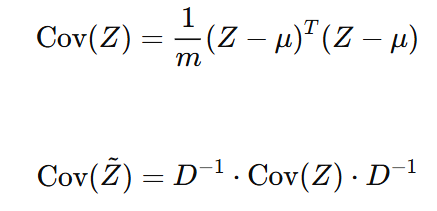
즉 기본적은 $Cov(Z)$에 $D^{-1}$ 연산이 추가된 형태임을 알 수 있습니다. 이는 diagonal component에 dimension의 분산 값이 1로 맞추어줌으로써 dimension의 scale을 조정합니다. 하지만, D는 diagnoal matrix임으로 off-diagonal component들은 직접적으로 건들지 않기 때문에, 결국 feature 간 correlation 문제를 근본적으로 풀어내지는 못합니다. 즉, 이는 엄연히 sub-optimal이고 근본적인 해결책이 되지는 않습니다. 하지만 저자는 이러한 batch normalization의 영향이 distillation에 매우 중요한 영향을 끼침을 언급하고 있습니다. 왜냐면 singular value의 collapse 문제는 간접적으로 풀어낼 수 있기 때문입니다. ( 어느 정도 dominant한 singular value의 영향력이 감쇄될 수 있음 ).
마지막으로 저자는 단순 L2 distance가 아닌 LogSum distance를 사용합니다. 수식은 아래와 같습니다.
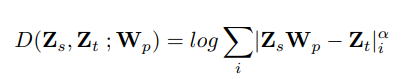
본 수식의 component의 역할을 설명하면 아래와 같습니다.
1) Log 적용 : 우선, student와 teacher 간의 capacity가 큰 경우 L2 distance가 안정적이지 않을 수 있기 때문에 log를 통해 scale을 안정화했다고 합니다.
2) Loss summation in batch : batch 내 오차들을 합산 함으로써 모든 sample에 신경을 쓰고자 했습니다. 이 때 평균이 아니라 합산을 쓰게 되면 오차가 큰 애들의 영향을 약간 더 받아들이게 됩니다.
3) alpha : 큰 error에 α배로 패널티를 줌으로써, 큰 오차에 훨씬 민감해지게끔 설계하였습니다. 저자는 경험적으로 4~5에서의 값이 성능이 좋았다고 합니다.
또한 본 논문은 Projection-head가 적절한 weight-decay를 주게 되면 마치 teacher의 relational information을 Momentum Encoder (moving average 와 같은 역할) 의 momentum update 처럼 수행할 수 있음을 언급합니다. 예를 들어, 아래 수식을 살펴보겠습니다.

본 수식에서는 $W_{p}$를 업데이트하기 위해 gradient 와 weight decay를 수행하는 부분이 나옵니다. 하지만 밑에 수식을 보면 마치 $W_{p}$가 기존의 과거 가중치에 현재 업데이트되는 gradient가 같이 고려되서 마치 moving average처럼 동작하게 됩니다. 즉 이는 Projection head는 단순한 feature aligner를 넘어서, 학습 과정에서 teacher가 가진 relational pattern을 점진적으로 평균내며 쌓아가는 momentum encoder처럼 동작함을 의미하게 됩니다. 이러한 기능을 내부적으로 하고 있기 때문에 단순한 dimension을 하는 것이 아니라 더 중요한 역할을 수행하게 됩니다. 물론 moving average의 효과도 있기 때문에 weight가 smooth하게 업데이트가 되게 됩니다.
여기까지 본 논문의 이론적 내용을 간단하게 요약했고, 의문점을 몇 가지 정리해보았습니다.
- Projection-head를 깊게 쌓아야지, 더 과거 sample과 relational information을 학습할 수 있지 않을까? 물론 input과 output의 정보 간의 차이가 발생할 수는 있지만 (저자는 큰 projection-head가 input과 output간의 정보의 gap을 만든다고 지적), 이러한 relation 정보가 중요하다면 더 큰 projection-head가 필요하지는 않을까?
- 추가적으로 backbone과 projection-head의 optimize 부분도 고민이 되어야하지 않을까? 본 논문은 같이 학습했지만 정말 같이 학습하는 것만이 최선일까? 둘이 학습을 수행하는 관점이 다르지 않나? 또한 student가 무언가로 initialize되어 있다면 이야기가 더 달라지지 않는가?
- 왜 layer normalization + group normalization 과 같은 방법은 비교를 하지 않았을까?
- 꼭 LogSum loss가 최선일까? Cosine similarity와의 ablation 비교는 왜 하지 않았을까? 비슷한 효과를 가졌다고 하면 직접적인 비교가 필요하지 않을까?
- 궁극적으로 Whitening Transformation이 중요한 거라면 이를 직접 역행렬을 계산하지 않고 learnable하게 만들 수는 없을까?
긴 글 읽어주셔서 감사합니다.
'ML & DL & RL' 카테고리의 다른 글
| 분포 거리에 대한 개념적 고찰 (KL Divergence, JS Divergence, Wasserstein Distance) (0) | 2025.04.29 |
|---|---|
| Gaussian Mixture Model 개인 공부용 (0) | 2025.02.16 |
| [Deep Learning] Activation function & Weight Initialization & Regularization (0) | 2022.10.18 |
| [Deep-Learning] 나만의 CNN 구현해보기 실습 (1) | 2022.09.30 |
| [Deep-Learning] 2D Convolution operation (2) | 2022.09.24 |




