No Limitation
[Paper Review] Deep Anomaly Detection with Deviation Network (2) 본문
( 본 논문은 카이스트 산업 및 시스템 공학과 박찬영 교수님 지식서비스를 위한 기계학습 수업에 참고가 되는 포스팅입니다, Reviewer: 조예성 )
본 포스팅의 양이 많아 총 2개의 포스팅으로 나누어 정리하려고 합니다.
본 논문에 대한 리뷰 영상도 제 개인 유튜브 채널에 올려놓았습니다.
글보다 영상이 더 편하신 분은 영상을 참고하시면 좋을 거 같습니다.
리뷰 영상 :
https://www.youtube.com/watch?v=1lEtPCn-lcY
본 리뷰는 크게 다음 5가지 주제를 바탕으로 정리를 하고자 합니다.
1. Anomaly Detection이 어떤 개념이고 무슨 task를 수행하고자 하는 건지
2. 본 논문의 방법이 제안된 배경
3. 방법론
4. 실험 결과 (유튜브)
5. 코드 리뷰 (유튜브)
본 포스팅에서는 본격적으로 위 논문에 대한 리뷰를 시작하겠습니다.
제 개인적인 해석이 오류가 있을 수 있는 부분도 있기 때문에 본 논문의 원문 문장도 같이 넣어 정리하겠습니다.
논문의 제목은 'Deep Anomaly Detection with Deviation Network'라는 논문으로 SIGKDD의 Knowledge Discovery & Data Mining에 2019년에 등재된 논문입니다.
2. 본 논문의 방법이 제안된 배경
우선 간단하게 논문의 Introduction부터 살펴보겠습니다.
AD task를 수행하는데 있어 본격적인 deep learning 방법이 적용되기 전까지 전통적인 방법은(SVM 같은) 다음과 같은 2가지 한계점에 직면하게 되었습니다.
- high dimensionality
- highly non-linear feature relation
첫 번째로 차원의 저주 문제가 있었고 두 번째로는 anomaly를 detect하기 위한 feature간의 linear하지 않은 관계로 인해 온전한 모형 설정이 어렵게 된 것입니다.
하지만 이러한 문제는 non-linear 방법을 바탕으로 한 neural net 방법이 등장하면서 위 문제를 해결하게 되었습니다. 하지만 neural net이 적용되고 나서 봉착하게 된 문제는 크게 2가지가 있었습니다.
- anomaly data가 매우 적다는 것
it is very difficult to obtain large-scale labeled data to train anomaly detectors due to the prohibitive cost of collecting such data in many anomaly detection application domains
- anomaly data 간의 유사성이 없다는 것
anomalies often demonstrate different anomalous behaviors, and as a result, they are dissimilar to each other, which poses significant challenges to widely-used optimization objectives that generally assume the data objects within each class are similar to each other
우선 labeled 된 anomaly data의 수가 매우 적다는 것과 그것들을 얻는 데에 cost가 많이 발생하게 됩니다.
또한 일반적으로 모형이 train data기반으로 학습을 수행하는데 학습한 anomaly 데이터와는 또 다른 형태의 distribution을 갖는 anomaly 데이터가 존재할 가능성이 크다는 것입니다.
그래서 현대 딥러닝 기반의 AD 모형은 supervised 방법이 아닌 unsupervised 방법을 적용하여 이 문제를 해결하려고 하였습니다.
바로 'Representation learning'을 활용하는 방법인데, 다음과 같은 two-step의 approach를 적용하였습니다.
1. They first learn to represent data with new-representation
즉, 데이터를 잘 표현할 수 있는 핵심적인 feature를 뽑아내는 방법을 학습하는 단계라고 할 수 있습니다.
2. They use the learned representations to define anomaly scores using reconstruction error or distance metrics space
그리고 Representation learning이 발전하게 되면서 AD에서는 2가지 컨셉의 metric을 적용하게 되는데, 이것이 지난 포스팅에서도 소개드렸던 'Reconstruction Error'와 'Distance-based measures'입니다.
ex) Intermediate Representation in AE, Latent Space in GAN, Distance metric space in DeepSVDD
하지만 저자는 이러한 two-step의 approach가 갖는 문제점으로서, representation learning을 하는 부분과 anomaly detection을 하는 부분이 separate되어 있다는 점을 지적합니다.
However, it most of these methods, the representation learning is separate from anomaly detection methods, so it may yield representations that are suboptimal or even irrelevant w.r.t specific anomaly detection methods.
또한 prior-knowledge의 부족으로 Unsupervised learning을 바탕으로 anomaly detection을 수행하는 경우, data noise나 uninteresting data를 anomaly 데이터로 인식하는 경우가 발생하게 됩니다.
이 문제에 대한 해결책으로 저자는 제한된 수의 labeled data를 활용해서 사전 지식이 부족한 문제를 보완할 수 있다고 제안합니다.
따라서 위 방법에 대한 문제점을 극복할 수 있는 방법으로 저자는 'Anomaly Scores'를 학습하는 end-to-end learning 방법을 제안하게 됩니다.
In this paper, we introduce a novel anomaly detection framework to fill these gaps by leveraging a few labeled anomalies to fulfill an end-to-end differentiable learning of anomaly scores

위 그림을 한번 살펴보겠습니다. (a)의 경우 기존 representation을 바탕으로 anomaly detection을 수행하는 방법을 도식화한 그림이고 (b)의 경우 본 논문에서 제안하는 방법의 도식도입니다. 위 그림에서 알 수 있듯 기존 방법은 데이터로부터 feature를 뽑아내어 이를 바탕으로 여러 metric을 적용 ( reconstruction error, distance metric ) 하여 detecting을 수행하게 됩니다. 하지만 저자는 이러한 부분이 indirect하게 모형을 optimize하는 것이라고 지적합니다. 하지만 (b)같은 경우는 데이터를 입력받으면 end-to-end로 바로 anomaly score를 도출하게 되어 detecting을 수행하게 됩니다. 즉, 모형을 direct하게 optimize할 수 있는 구조라고 언급합니다.
또한 본 논문에서 제안하는 방법의 또 다른 novelty는, anomaly의 정도를 판단할 수 있는 reference score를 정의하였다는 점입니다. 즉, normal data로부터 추출된 평균적인 anomaly score와 현재 입력 간의 deviate된 정도를 바탕으로 판단을 한다는 점에서 기존 방법에서 갖는 방법과 차별된다는 점을 언급합니다.
따라서 본 논문이 갖는 novelty를 다음과 같이 2가지로 정리할 수 있습니다.
1. With the original data as inputs, we directly learn and output the anomaly scores rather than the feataure representations.
2. Define the mean of anomaly scores of some normal data objects based on a prior probability to serve as a reference score for guiding the subsequent anomaly score learning.
3. 방법론
자 그러면 본격적인 methodology를 살펴보도록 하겠습니다.
End-to-End Anomaly Score Learning
위에서 언급한 prior knowledge가 부족한 문제를 해결하기 위해 unlabeled 데이터와 limited labeled 데이터를 혼재한 데이터셋을 사용합니다.

N의 경우 unlabeled 데이터의 수를 의미하여 K의경우 매우 소량의 labeled된 anomaly 데이터를 의미합니다.
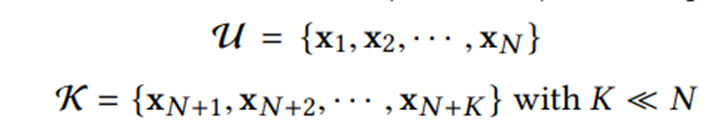
이렇게 데이터를 세팅하게 되면,
우리의 가장 큰 목적은 바로 anomaly score를 도출하는 이 파이 함수를 잘 학습해서 anomaly와 normal 간의 anomaly scoring 차이를 만드는 것을 목적으로 하게 됩니다.


그렇다면 거시적인 Framework부터 살펴볼까요?

우선 'Anomaly Scoring Network'이라고 하는 anomaly score를 도출하는 네트워크 하나와 Reference score를 generate하는 부분으로 크게 2개의 아키텍처를 가짐을 알 수 있습니다.
Anomaly score를 도출하는 네트워크의 경우 2개의 세부적인 구조를 가짐을 알 수 있는데, input이 들어오고 나면 representation을 만드는 'Intermediate representation' layer와 이를 바탕으로 곧바로 anomaly score를 도출하는 layer로 구성이 되어 있습니다. 이에 대한 구체적인 구조는 뒤에서 자세하게 다루겠습니다.
그리고 Reference score를 도출하는 부분은 R = { x1, .., xl }을 보면 l개의 random sample을 뽑게 되는데 이 샘플들은 normal 데이터에서 뽑은 임의의 샘플들이고 이들의 평균을 계산한 µ_r 을 이용하여 이들로부터 떨어진 정도로 anomaly를 판단하는 방법으로 모형이 동작하게 됩니다.
그러면 구체적으로 어떻게 구현되는지 살펴보겠습니다.
Deviation Networks
저자가 제안한 방법을 한 문장으로 요약하면 다음 문장으로 정리할 수 있을 것 같습니다.
"The proposed framework is instantiated into a method called Deviation Networks (DevNet), which defines a Gaussian prior and a Z Score-based deviation loss to enable the direct optimization anomaly scores with an end-to-end neural anomaly score learner"
다음 빨간색의 단어들이 핵심 아키텍처를 이루는 부분인데요. 우선, 첫번째 Deviation Network의 backborn을 이루는 Anomaly Scoring Network부터 살펴보도록 하겠습니다.

Anomaly Scoring Network는 ∅함수로 나타낼 수 있는데, 이는 크게 Intermediate representation space인 Q를 만드는 ψ네트워크와 anomaly score를 나타내는 η 네트워크로 구성이 됩니다.
- Intermediate representation space (Q)

- Total anomaly scoring network

이 ∅ 네트워크를 구성하는 2가지 sub network
[1] Q를 만드는 ψ 네트워크 ( feature learner )

[2] Q에서 anomaly score를 도출하는 η 네트워크 ( anomaly score learner )

그리고 ψ 네트워크는 Feature learner로서 H개의 hidden layer로 구성.

따라서 다음과 같이 표기를 가능.

Feature learner를 구성하는 hidden layer는 들어오는 input, 수행하려는 task에 따라 다르게 구성됩니다. 가령 이미지 데이터를 feature representation을 해야 하는 경우는 CNN 네트워크를, sequence data같은 경우는 RNN 네트워크를 사용하게 됩니다.
그리고 η 네트워크의 경우 simple linear neural unit을 사용해서 스코어를 계산하도록 네트워크를 구성하였습니다.
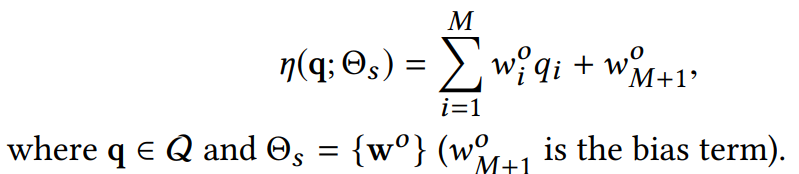
따라서 다음과 같이 전체 anomaly scoring network를 구성할 수 있게됩니다.

저자는 이와 같은 방법을 통해 기존의 방법과 달리 direcly하게 data를 anomaly score로 mapping할 수 있다고 주장합니다.
Which directly maps data inputs to scalar anomaly scores and can be trained in an end-to-end fashion.
자 그러면 이와 같은 방법으로 anomaly score를 도출하게 되는데, 여기서 그냥 그치면 뭔가 아쉽겠죠.
저자는 여기서 추가적으로 이 score가 정말 anomaly한지 안한지를 같이 참고할 수 있는 reference score를 구축하는 방법을 제안하게 됩니다.
기본적으로 이 reference score는 normal objects인 R에서 랜덤으로 뽑아 그 score를 기준으로 optimization에 활용하는 방식으로 동작하게 됩니다.
이 방법을 수행하는 방법으로는 2가지로 접근할 수 있다.
1. Data-driven approach
2. Prior-driven approach
우선 Data-driven 방법은 학습 데이터 X를 기반으로 하여 anomaly score를 도출하여 평균을 계산한 µ_r 를 도출해 활용하는 방법입니다. 하지만 이 방법은 제한이 많은데, 바로 이 µ_r 이 X 값이 바뀔 때 마다 조금씩 변하는 특징이 있기 때문입니다.
그래서 본 논문에서는 사전 확률 F에서 추출하는 reference score를 바탕으로 µ_r 를 계산하는 방법을 채택하였습니다. 그 이유로 저자는 2가지 이유를 설명합니다.
1. The chosen prior allows us to achieve good interpretability of the predicted anomaly scores
2. It can generate µ_r constantly, which is substantially more efficient than the data-driven approach
첫 번째로 다음과 같은 방법이 anomaly score를 예측할 시 good interpretability(좋은 해석?)을 갖는다고 합니다. 또한 µ_r 을 constant하게 고정할 수 있는 장점이 있습니다.
하지만 잘 와닿지가 않죠. 사전 확률 F라는 것이 대체 무엇인지 감을 잡을 수 없으니까요.
본 논문에서는 바로 이 사전 확률 F라는 것을 가우시안 분포를 차용하게 됩니다.
가우시안 분포를 사용하면 정말 normal data의 anomaly score를 잘 대변할 수 있을까요?
저자는 다음과 같이 주장합니다.
Gaussian distribution fits the anomaly scores very well in a range of data sets. This may be due to that the most general distribution for fitting values derived from Gaussian or non-Gaussian variables is the Gaussian distribution according to the central limit theorem.
즉, 앞서 AD task에서 대부분의 데이터는 normal이라는 이야기를 하였습니다. 그러면 이 normal 데이터들에 대한 anomaly score들도 어떠한 distribution을 따르게 되겠죠. 이 점수들 또한 sample들을 충분히 뽑게 되면 이 친구들도 gaussian distribution을 따르게 될 겁니다. 바로 Central Limit Theorem 때문이죠.
즉, 다음과 같은 그림으로 쉽게 이해해볼 수 있습니다.
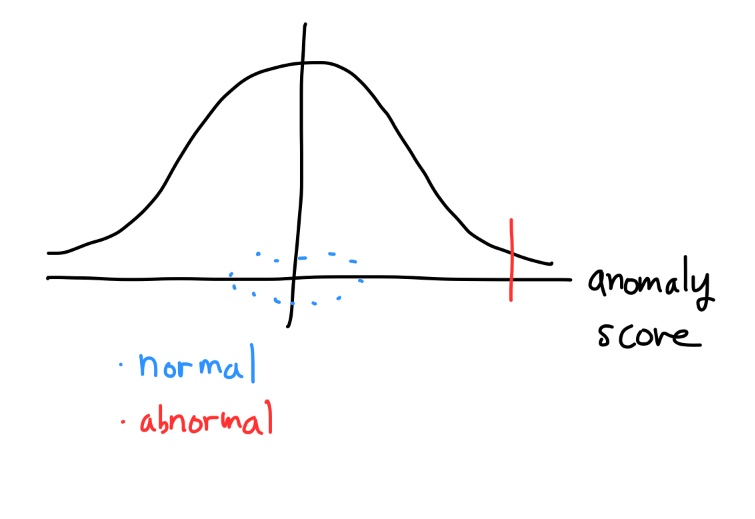
즉, normal 할수록 µ_r 에 더 가까운 점수를 형성하게 될거지만 abnormal할 수록 µ_r로부터 더 거리가 있는 점수가 나오겠죠. 이러한 deviation 정도를 사용하여 loss function을 정의하게 됩니다.
µ_r
따라서 reference score로 활용할 수 있는 데이터들을 다음과 같이 도출하게 됩니다.

저 각각의 ri는 정규 분포에서 도출하며 저 ri는 랜덤한 normal 데이터 객체의 anomaly score를 의미하게 됩니다. 본 연구에서는 µ_r을 0, σ_r를 1로 설정하였으며, 랜덤 샘플은 CLT를 만족할 수 있는 충분한 양이면 전부 사용 가능하다고 명시합니다. 저자는 5000개의 샘플을 사용하였습니다.
자 그러면 이러한 reference score를 바탕으로 구체적으로 어떻게 loss function을 정의하는 지를 살펴보도록 하겠습니다. 본 논문에서는 deviation 정도를 측정하는 지표를 Z-score 방법을 차용해서 표현하고 있습니다. 아래의 loss를 저자는 contrastive loss라고 명명합니다.

예를 들어 normal 데이터면 저 ∅ 값이 µ_r이랑 근사하게 되겠고 abnormal 데이터면 그렇지 않겠죠.
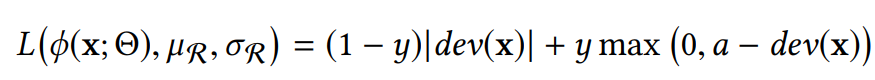
x가 anomaly인 경우 y = 1, x가 normal인 경우 y = 0이 됩니다.
그리고 위 'a'의 경우 Z-score의 confidence interval paramter 가 됩니다.
이게 무슨 말일까요?
다시 한 번 구체적으로 term을 살펴보겠습니다.

Note that if x is an anomaly and it has a negative dev(x), the loss is particularly large, which encourages large positive derivations for all anomalies.
만약에 x가 anomalies인데 deviation이 음수이면 전체 loss 값은 커지게 됩니다. 따라서 모형은 이 anomaly data의 deviation이 큰 양수 값을 가지게끔 만들려고 하게 됩니다. 거의 a값에 근사해질 만큼으로 말이죠.
이 말의 의미는 다음 그림으로도 쉽게 이해할 수 있습니다.
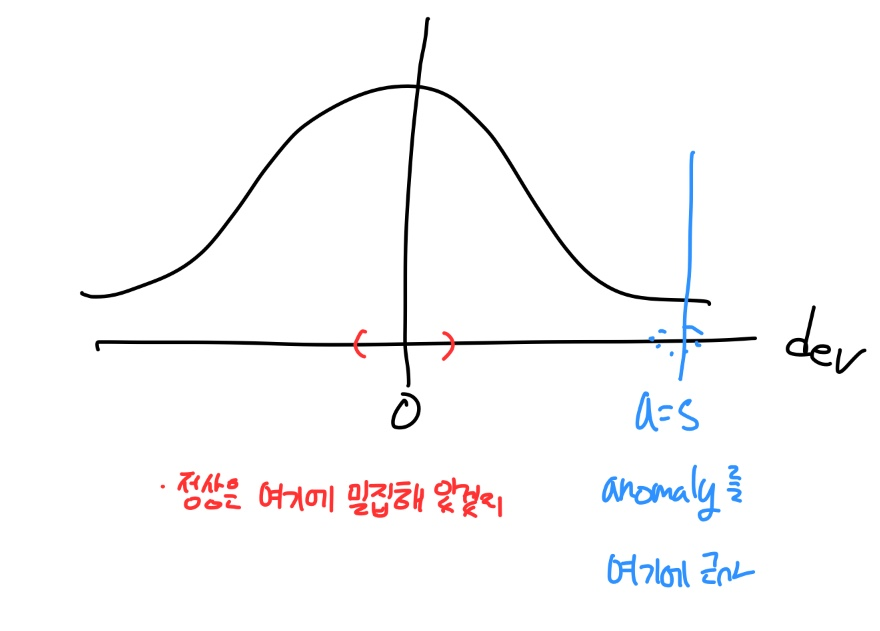
즉, dev 값이 0 근처로 오는 경우는 정상 데이터들이지만 a=5로 주었을 때는 이 경우 anomaly를 저 곳으로 근사시키는 경우로 적용시킬 수 있습니다. 본 논문에서도 a=5로 주어 사용했다고 하네요
원문은 정확히 다음과 같이 언급하고 있습니다.
Therefore, the deviation loss is equivalent to enforcing a statistically significant deviation of the anomaly score of all anomalies from that of normal objects in the upper tail. We use a = 5 to achieve a very high significane level for all labeled anomalies.
하지만 여기서 분명 물음표를 찍으시는 분들이 계실 겁니다. 자꾸 normal, normal하는데 애초에 우리는 limited된 anomalies를 제외하면 어떤 normal labeled 데이터를 모르는 상황인데, 왜 normal 데이터를 언급하냐는 부분이 궁금하실 겁니다. 사실 이건 다음과 같이 해결합니다.
We address this problem by simply treating the unlabeled training data objects in U as normal objects.
즉 그냥 normal 데이터로 간주하는 것입니다. Unlabeled 데이터가 전부 normal이라는 보장이 있는 것도 아니면서도 말이죠 ( 실제 Unlabeled 데이터에 abnormal이 들어있는 경우를 contaminated 되었다고 표현합니다 )
굉장히 이상하죠...! 왜 그렇게 할까요?
사실 공부하다보면 많은 semi-supervised learning에서는 Unlabeled된 데이터를 전부 normal이라고 치부하여 모형을 fitting하게 됩니다. 사실 그 이유는 2가지가 있는데 처음으로는 이것이 실제 real world와 굉장히 유사한 상황이기 때문입니다. 실제로도 우리는 많은 labeled 되지 않는 데이터가 존재합니다. 하지만 우리는 알듯, anomaly한 상황은 굉장히 scarce하게 발생하게 됩니다. 즉 대부분의 가지고 있는 데이터는 normal하다는 전제가 들어가는 것이죠. 따라서 이러한 real world 상황을 그대로 고려해주는 조치인 것입니다. 또한 이 매우 적은 anomaly 데이터가 실제 backpropagation을 수행할 때 SGD 기반의 optimization에 대해서는 그다지 영향력이 크지 않다는 것을 전제합니다. 즉, 모형의 성능에 그렇게 큰 영향을 주지 않을 것이라는 거죠. 따라서 거의 rule of thumb 식으로 semi-supervised learning에서는 unlabeled 데이터를 normal이라고 간주해서 사용하곤 합니다. ( 물론 이 부분에 대해서도 더 연구가 되어야할 것으로 보입니다. )
따라서 다음과 같이 DevNet 알고리즘을 슈도 코드로 정리할 수 있습니다.

그렇다면 이제 loss function까지 디자인하여 training할 준비가 되었으니 다음으로 check 해봐야하는 부분은 바로, 'Interpretability'입니다. 즉, 어떤 경우일 때 normal, abnormal이라고 판단하냐는 거죠.
본 연구는 다음 Proposition을 사용합니다.
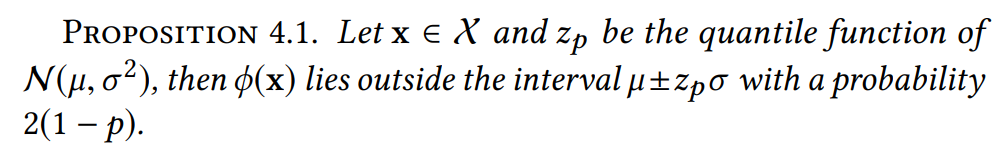
이 말의 의미가 뭘지 한번 생각해봅시다.
일반적인 표준정규분포에서는 다음과 같은 성질이 있죠.
만일 µ_r가 0이고 σ_r가 1인 정규분포가 있고, p=0.95라고 하면, z(0.95)=1.96이 되므로=
µ_r = 0을 기준으로 ( µ_r - z ~ µ_r + z ) 구간이 결국 신뢰 구간이 됩니다.
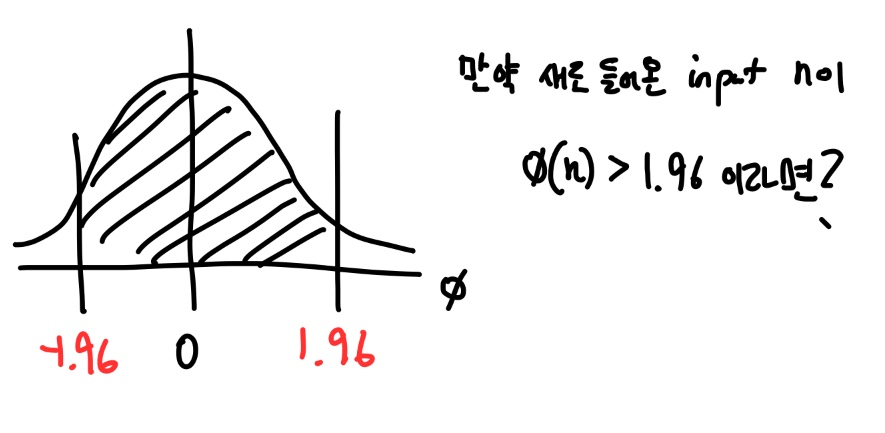
하지만 만약 새로 받은 anomaly score가 이 boundary를 넘어가는 곳에 mapping이 된다면 어떨까요? 그 의미는 결국 다음과 같이 생각할 수 있습니다.
The object only has a probability of 0.05 generated from the same machanism as the normal data objects.
즉, normal 일 확률이 매우 낮게 되는 것입니다.
왜 이런 form을 기준으로 anomaly를 판단하는 threshold를 설정했냐면,
This proposition of DevNet is due to the Gaussian prior and Z-Score-based deviation loss.
즉, Z-score 기반의 deviation loss를 정의했기 때문입니다.
이렇게 학습이 수행되게 됩니다.
Experiment
( 기존 포스팅에서 Experiment 내용을 추가하지 않았었는데, 추가하는 방향으로 포스팅을 수정하였습니다. )
본 논문에서는 9가지의 real-world 데이터셋을 사용합니다. 구체적으로는 다음과 같은 데이터셋을 사용합니다.
- Fraud Detection ( fraudulent credit card transaction )
- Malicious URLs in URL
- The thyroid disease detection
...
자세한 사항은 저자가 Appendix에 추가해놓은 아래 링크를 참고하면 좋을 것 같습니다.

비교 집단으로 사용한 모형은 다음과 같습니다.
[1] REPEN
[2] adaptive DeepSVDD
[3] Prototypical Network (FSNet)
[4] iForest
REPEN의 경우 limited labeled data를 사용하는 neural net 기반의 AD network이고, FSNet의 경우 few show classification을 수행하는 네트워크입니다. 두 네트워크 모두 limited labeled 데이터를 사용하는 것이 특징입니다. DevNet과 동일한 조건이죠. 반면 Unsupervised 방법으로 AD를 수행하는 앙상블 기반의 모형 iForest도 비교집단으로 사용하였습니다.
DeepSVDD 같은 경우는 굉장히 유명한 AD를 수행하는 알고리즘인데요, 여기서 저자는 어떠한 조작을 가해 DeepSVDD를 DevNet과 비교할 수 있는 조건으로 만들어 놓습니다. 바로 semi-supervised learning을 할 수 있는 형태로 만드는 것이죠.
We modified DSVDD to fully leverage the labeled anomalies by adding an additional term into its objective function to guarantee a large margin between normal objects and anomalies in the new space while minimizing the c-based hypershere's volume.
즉, labeled된 anomalies를 사용할 수 있는 형태로 loss function을 조금 adjust했다고 언급합니다. 그리고 실제로 이러한 수정하는 과정을 거침으로서 original SVDD보다 더 성능이 잘 나왔다고 언급합니다.
아시는 분도 계시겠지만 DeepSVDD의 semi-supervised learning 버젼은 2019-2020년에 동일한 저자가 작성한 DeepSAD이라는 방법이 있습니다. 하지만 DevNet이 나올 땐 아직 DeepSAD이 나오기 전이기 때문에 당시 DevNet 저자는 이러한 heuristic을 적용했던 것 같습니다.
이렇게 총 4개의 비교 집단을 사용하여 성능을 비교하였습니다.
Metric은 어떻게 될까요?
일반적으로 AD에서 사용하는 metric은 AUROC와 AUC-PR을 사용합니다.
이 둘에 대해서는 간략하게 정리해보도록 하겠습니다.
- AUROC ( Area Under Receiver Operating Characteristics )
많이들 알고 계시는 ROC curve입니다. 이 ROC curve를 이해하기 위해서는 우선 Confusion Matrix를 이해할 필요가 있습니다.

actual은 말 그대로 실제 label 값이고 pred는 prediction의 결과입니다. 다음과 같은 상황에서 우리는 True Positive, True Negative, False Positive, False Negative를 정의할 수 있고 이 수치들을 사용해서 다음과 같은 특징들을 정리할 수 있습니다.
Sensitivity ( 민감도, True Positive Rate ) = ( True Positive ) / ( True Positive + False Negative )
Specificity ( 특이도, True Negative Rate ) = ( True Negative ) / ( False Positive + True Negative )
False Positive Rate = ( False Positive ) / ( False Positive + True Negative )
Precision ( 정밀도 ) = ( True Positive ) / ( True Positive + False Positive )
Recall ( 민감도 ) = ( True Positive ) / ( True Positive + False Negative )
Accuracy ( 정확도 ) = ( True Positive + True Negative ) / ( True Positive + True Negative + False Negative + False Positive )
이 개념들 중에서 TPR(True Positive Rate)과 FPR(False Positive Rate)을 사용하여 Curve를 그리면 다음과 같은 Curve를 그릴 수 있습니다.
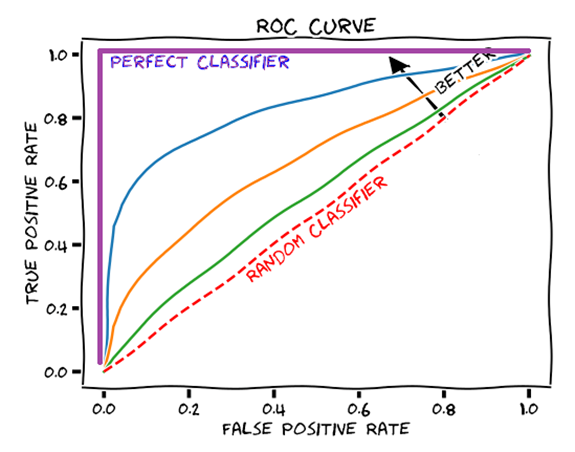
빨간 점선처럼 선이 형성되는 경우 random하게 classifier한 경우와 동일합니다. 그리고 빨간 점 아래에서 영역이 형성되는 경우는 0.5죠. 반면 보라색의 선의 경우 가장 모형이 강력한 경우, 즉 모든 경우를 맞춘 경우로 아래 면적은 1이 됩니다.
바로 이 면적의 크기에 따라 성능을 측정하는 것이 바로 AUROC입니다.
하지만 이러한 방법은 한계가 있습니다. 바로 minor class의 error에 대한 비중이 낮게 잡기 때문인데요.
감이 잘 안오시죠?
이해를 위해 예를 살펴보겠습니다.
예를 들어 normal 데이터가 30,000개, abnormal 데이터가 100개 있는 데이터를 본다고 해봅시다.
여기서 똑같이 50개를 틀린다고 하면, normal에서는 50개 틀린 것이 상대적으로 적게 되지만, abnormal에서는 50개가 틀리면 전체 2분의 1이 틀리는 것이기 때문에 적은 수치라고 볼 수 없습니다. 즉 이 틀리는 정도를 갖게 해서는 안되는 것입니다.
이러한 부분을 잘 반영해주는 것이 바로 Precision과 Recall의 조합입니다.
이 둘의 조금 더 명확한 이해를 위해 다음 예시를 들어보겠습니다.
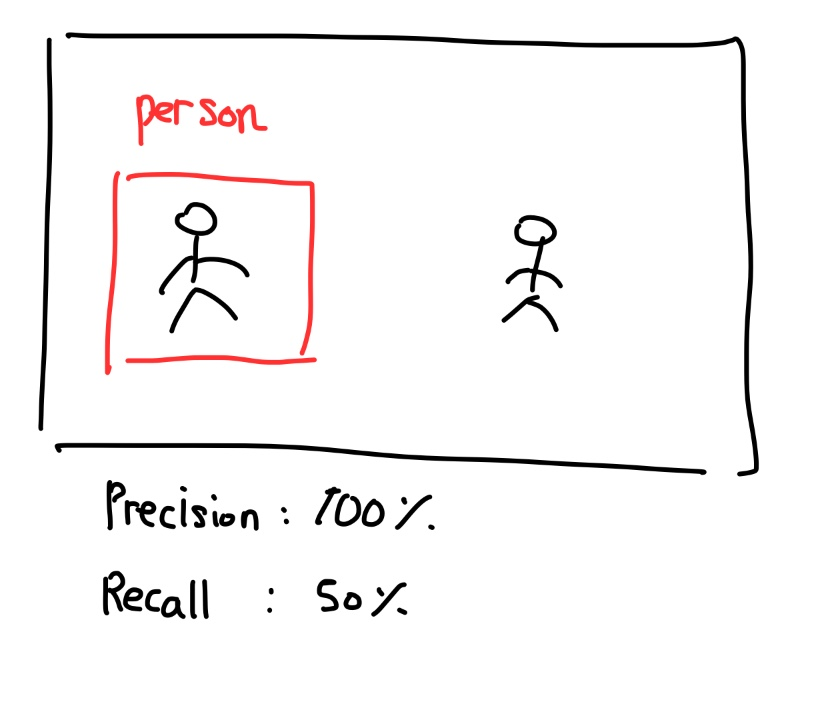
Object Detection을 수행하는 task를 예로 들어보죠. 여기서 모형이 다음과 같이 사람 2명이 있는 사진에서 한 사람을 탐지하고 이를 사람이라고 예측을 해봤다고 해봅시다. Precision 관점에서는 내가 예측을 시도한 경우가 다 잘 들어맞았다고 생각해서 100%의 정확도를 갖는다고 이야기합니다. 하지만 Recall 관점은 조금 다르죠. 사람이 실제로 한 명 더 있는데 이 사람은 맞추지를 못했으니 정확도는 50%이라고 이야기하는 겁니다.
즉 이 다른 두 관점을 적절하게 조합하여 metric을 만들면 위와 같은 문제를 극복할 수 있다고, 즉 minor한 class에 대해 더 적절한 가중치를 줄 수 있다고 판단한 것입니다. 이로부터 나온 개념이 바로 AUC-PR입니다.

자 그럼 다시 본론으로 돌아와서, 실험에 대한 구체적인 내용을 살펴보겠습니다.
우선 실험 환경 설정은 다음과 같이 설정하였습니다.
신경망의 깊이는 한 개의 hidden layer를 사용하였고 구체적인 파라미터 설정은 다음과 같이 설정하였습니다
- 20 neural units
- RMSProp Optimizer
- 20 mini batch
- ReLU
- L2 Norm Regularize
또한 network은 대부분의 데이터가 unordered multidimensional data라는 점을 고려하여 Multilayer perceptron을 사용하였습니다.
이러한 설정을 바탕으로 모형 간 성능을 비교한 결과는 아래와 같습니다.

census 데이터를 제외하고는 모든 경우에서 AUROC와 AUC-PR 모두 DevNet의 성능이 가장 우수함을 확인할 수 있었습니다.
본 그림에서 Data Characteristic에서 나온 notation의 의미는 다음과 같습니다.
# obj -> 데이터의 수
D -> 데이터의 dimension
f1 -> 학습 데이터에서 anomaly 데이터 비중
f2 -> 전체 데이터에서 anomaly 데이터 비중
을 각각 의미합니다.
하지만 여기서 끝나면 뭔가 아쉽죠.
저자는 구체적인 여러 실험을 통해 DevNet의 효율성을 검증합니다.
[1] Data Efficiency
첫 번째로 저자는 다음과 같은 궁금증을 해결하고자 하였습니다.
- How data efficient are the DevNet and other deep methods?
- How much improvement can the deep methods gain from the labeled anomalies compared to the unsupervisd iForest?
즉, 얼마나 본인들의 모형이 label이 추가되는 anomlies를 잘 활용하냐, prior knowledge를 잘 활용하냐를 측정하고자 하였습니다.
이 때 base line으로 사용된 iForest의 경우 labeled이 없기 때문에 label을 주든 안주든 모형의 성능 차이는 없게 됩니다.
다음 그림을 살펴보겠습니다.
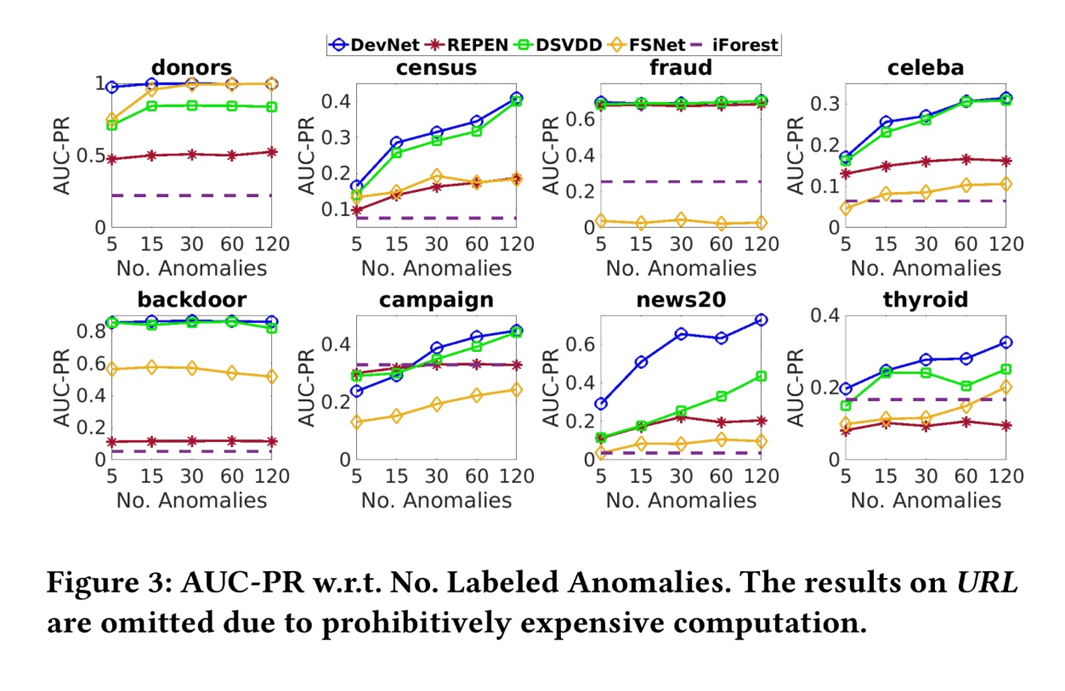
추가되는 anomalies의 수에 대해 가장 높은 성능을 DevNet이 보임을 알 수 있습니다. 특별히 campaign, census, news20, thyroid 데이터에 대해서 추가되는 anomalies label에 대해 더 큰 폭의 성능의 향상을 보임을 확인할 수 있었습니다.
[1] Robustness w.r.t. Anomaly Contamination
두 번째로는 anomaly contamination에 대해 얼마나 강력한 대응을 수행하냐입니다.
앞에서 잠깐 언급했었지만 Contamination이 정확히 뭘까요? 다음 글을 참고해봅시다.
To confuse data by sampling anomaly and adding it to the unreliable training data or removing some anomaly
즉 일반적인 unlabeled 된 데이터를 normal 로 간주하는 상황에서 그 unlabeled된 데이터에 anomaly 비중이 contamination된 정도를 나타냅니다. 바로 이 양을 늘려감에 따라 모형이 얼마나 sensitive한 지를 측정한 결과입니다.
저자는 0~20% 정도로 contamination을 주면서 성능의 변화를 측정하였습니다.
다음 그림을 참고해봅시다.

대체적으로 attack에 대해 robust한 성능을 유지함을 확인할 수 있습니다.
다만 의문점은 'news20' 데이터셋에서는 유달리 DevNet이 drastic한 감소를 보임을 알 수 있었습니다. Text data로 구성된 news20에 대해 contamination에 대해서는 상대적으로 더 큰 감소폭을 보임을 알 수 있었습니다.
[3] Ablation Study
세 번째로 ablation study를 수행합니다.
저자는 DevNet의 아키텍처에 사용되는 여러 구성요소 { intermediate representation, FC layer, One hidden layer } 같은 것들이 실제 각각의 역할을 수행하는 지를 검증하였습니다. 저 요소들이 꼭 다 필요한 지를 확인하고자 한거죠.
그래서 총 3개의 비교 집단을 만들게 됩니다. 조금 더 간단하게 도식화해보면 다음과 같습니다.

즉, 기존의 Def가 DevNet이라면, 각각의 구성 요소를 하나씩 제거하거나 layer를 3개로 늘리는 조작을 가하게 됩니다.
DevNet-Rep의 경우 마지막에 anomaly score를 scala 형태로 도출하는 FC layer를 제거하였습니다. 즉 20개의 dimension을 갖는 벡터를 바탕으로 성능을 도출하게 되는거죠. ( 이부분에서 어떻게 anomaly score를 도출했는 지가 명확히 언급되어 있지 않네요. ) DevNet-Linear의 경우 feature representation을 수행하는 network를 제거하고 바로 linear함수를 통해 anomaly score를 도출하게 됩니다. 마지막으로 DevNet-3HL은 3개의 hidden layer는 20개의 ReLU를 사용하는 하나의 layer가 아닌 1000 - 250 - 20 개의 ReLU를 사용하는 3개의 hiddne layer로 구성합니다.
이에 대한 성능의 결과는 다음과 같습니다.
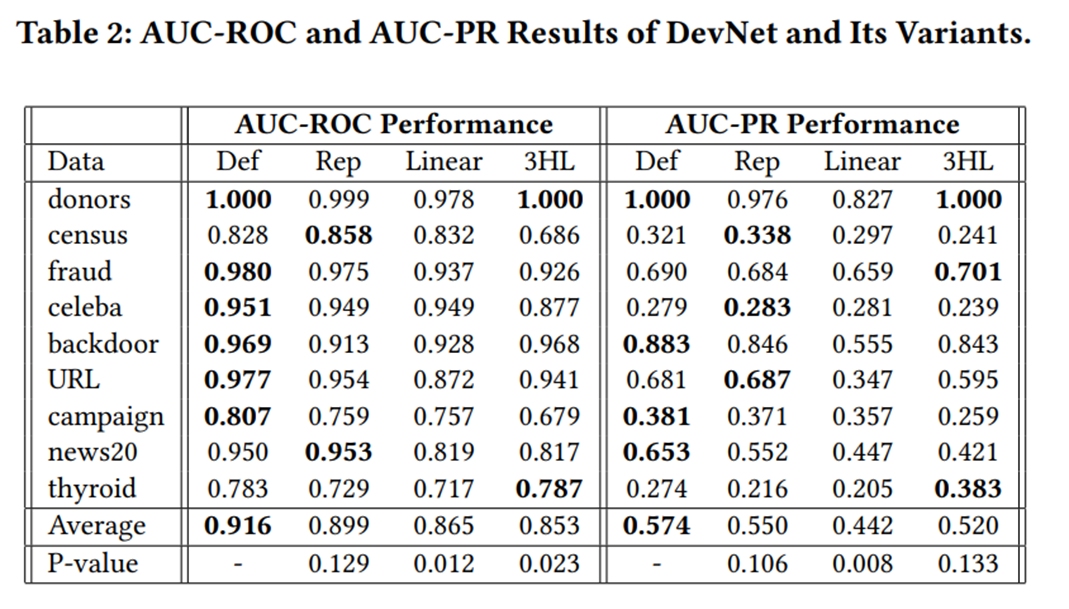
대부분의 데이터셋에서 AUROC는 본 DevNet의 성능이 우수하였습니다. 하지만 AUC-PR의 경우 일부분에서 Rep나 3HL이 더 우수하게 나온 경우도 존재하였음을 알 수 있습니다. 특히 census 데이터의 경우는 Rep에서 성능이 가장 우수했음도 확인할 수 있었습니다.
하지만 대체적으로 Def의 성능이 가장 우수하였으므로 end-to-end learning을 구축하는 각각의 요소들이 전부 적절한 contribution을 갖는다고 설명합니다.
또한 3HL 같이 더 깊은 신경망을 적용한 것이 왜 더 잘 동작하지 않는 지를 설명하는데, 이 이유로, 매우 적은 labeled anomalies를 매우 깊은 신경망을 쌓게 되면 그 특징을 놓치기 쉽다는 부분을 언급합니다. 즉, 대부분의 normal 데이터가 데이터를 이루는 상황에서 신경망을 깊게 쌓게 되면 anomalies의 특징을 잃기 때문입니다. 따라서 저자는 one-hidden layer가 가장 fit하다는 것을 설명합니다.
[4] Scalability
마지막으로 데이터의 size와 dimension에 따른 수행 시간이 어느정도 되는지, 즉 complexity를 확인하기 위한 실험을 추가적으로 진행하였습니다. size를 고정시켜놓고 dimension의 변화에 따른 수행 시간을 측정하였고 dimension을 고정시켜놓고 size의 변화에 따른 수행 시간을 측정하였습니다. 이에 대한 결과는 다음 그림과 같습니다.

대부분의 모형에서 linear time이 소모되었지만, DevNet의 경우 data size에 대해서는 크기가 10만이 넘어가는 영역에서도 준수한 속도를 보임을 확인할 수 있었습니다. dimension에 대해서도 FSNet보다는 느리지만 다른 타 모형에 비해 더 빠른 성능을 보임을 알 수 있었습니다.
Conclusion
따라서 본 논문이 제기하는 Contribution에 대해 정리하면 다음 3가지로 정리할 수 있습니다.
1. This paper introduces a novel framework and its instantiation DevNet for leveraging a few labeled anomalies with a prior to fulfill and end-to-end differentiable learning of anomaly scores
대부분의 Unsupervised learning의 한계점을 극복하기 위해 적은 소량의 limited anomaly labeled 데이터를 사용했단느 점
2. By a direct optimization of anomaly scores, DevNet can be trained much more data-efficiency, and performs significantly better in terms of both AUROC and AUC-PR compared other two-step deep anomaly detectors that focus on optimizing feature representations
기존 representation 영역과 detecting 영역이 two-step으로 구분됨으로서 indirect하게 optimize하는 것이 아니라 direct로 optimize하는 방법을 제안한다.
3. Deep anomaly detectors can be well trained by randomly sampling negative examples from the anomaly contaminated unlabeled data and positive examples from the small labeled anomaly set.
또 다른 측면은 바로 normal distribution을 바탕으로 한 reference score를 사용하여 anomaly 정도를 측정하려고 한 점도 독특한 접근이라고 판단할 수 있었습니다.
코드 리뷰
코드 실습에 대해서는 포스팅으로 정리하는 것에 의미가 크지 않다고 생각하여 추가적으로 학습을 하시고자 하는 분들에게는 녹화해놓은 유튜브 영상의 좌표를 남깁니다. 따로 정리하지 못한 점 양해부탁드립니다..!
https://www.youtube.com/watch?v=1lEtPCn-lcY
코드 리뷰 : 55:30 ~ 끝까지
지금까지 DevNet 리뷰였습니다!!
긴 글 읽어주셔서 감사합니다!!




