[Graph] Bellman-Ford Algorithm, 최소비용 구하기 - 백준

https://www.acmicpc.net/problem/1916

1916번: 최소비용 구하기

 

다음 문제를 접근하는 2가지 방법으로 Bell-man Ford 알고리즘과 Dijkstra 알고리즘을 사용하였습니다. 

 

다익스트라의 개념 같은 경우 지난 포스팅에서 이미 다룬 바 있으므로 

이번 포스팅에서는 Bell-man 알고리즘에 대한 개념 내용과 함께 

 

본 문제의 풀이에 적용해보도록 하겠습니다. 

 

About Bellman-ford,

개념 정리는 다음 포스팅들을 참고하였습니다. 

https://ratsgo.github.io/data%20structure&algorithm/2017/11/27/bellmanford/

벨만-포드 알고리즘 · ratsgo's blog

https://velog.io/@younge/Python-%EC%B5%9C%EB%8B%A8-%EA%B2%BD%EB%A1%9C-%EB%B2%A8%EB%A7%8C-%ED%8F%AC%EB%93%9CBellman-Ford-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98

[Python] 최단 경로 - 벨만 포드(Bellman-Ford) 알고리즘 구현하기

 

 

우선 벨만 포드는 기본적으로

[1] directed graph

[2] negative weight가 존재할 때 사용 가능

 

이 2가지를 전제로 합니다.

[1], [2]가 다익스트라에서는 적용이 안되는 점을 반영해 이 문제를 밸만 포드는 풀 수 있다는 장점이 있습니다. 다만, 시간 복잡도는 다익스트라보다 더 큰 알고리즘이 됩니다.

 

우선 최단 경로는 s에서 d로 가는 경로가 있을 때, s에서 d로 가는 것 자체의 경로가 최단 경로가 될 수도 있고, d를 제외한 다른 노드들이 s에서 d로가는 최단 경로를 구축할 수도 있습니다. 

즉, edge relaxation을 V-1번 수행을 하는 것을 의미합니다. 

 

출처 : https://ratsgo.github.io/data%20structure&algorithm/2017/11/27/bellmanford/

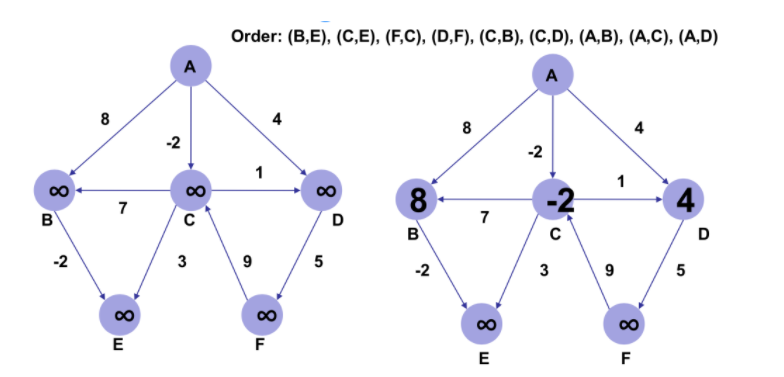
다음의 예시를 살펴보겠습니다. 우선 시작노드를 제외하고 모든 노드의 거리를 무한대로 초기화합니다. 위 'Order;의 경우 directed edge를 의미하며 저 위에 나와있는 edge들에서 edge relaxation을 수행하겠습니다. 우선, (B, E)의 경우 현재 edge relaxation을 수행할 수 없습니다. (C, E) .. (C,D)까지 마찬가지게 되고 시작 노드 A부터 즉, (A,B), (A,C), (A,D)는 edge relaxation이 수행되게 됩니다. 이 경우 오른쪽 그림처럼 무한대에서 각각 8, -2, 4로 edge relaxation이 수행됨을 확인할 수 있습니다. 이 상태에서 1차 루프가 종료됩니다. 

출처 : https://ratsgo.github.io/data%20structure&algorithm/2017/11/27/bellmanford/

다음 루프를 돌아보겠습니다. 이번에는 (B, E)에서는 edge relaxation을 수행할 수 있기 때문에 수행해줍니다. 이 과정을 V-1번 만큼 수행을 해줍니다. 

 

하지만 밸만 포드에서는 중요한 확인 과정이 있습니다. 바로 negative weight로부터 발생할 수 있는 negative cycle입니다. 

 

출처 : https://ratsgo.github.io/data%20structure&algorithm/2017/11/27/bellmanford/

 

다음 그림에서 c, d와 e,f가 cycle이 발생했는데 c,d에서 순회하는 결과 총 weight의 합이 3이 되서 cycle이 되도 전체 결과에 지장이 없지만, e, f의 경우 전체 weight가 -3이 되서 음수가 발생해 사이클을 돌면 돌수록 그 거리가 작아져 유의미하지 않은 결과를 도출하게 됩니다. 그래서 밸만 포드 알고리즘에서는 이러한 음수 사이클을 체크하는 과정을 추후에 별도로 거칩니다. 

 

 

밸만 포드 알고리즘의 시간복잡도는 모든 vertex에 대해 edge relaxation을 수행해는 것이 최악의 경우이므로 O(VE)가 됩니다. 고로 greedy하게 edge relaxation을 하는 다익스트라에 비해 코스트가 더 큰 알고리즘입니다. 

 

다시 그럼 위 백준 문제를 두 알고리즘을 놓고 풀어보겠습니다

 

[1] 밸만 포드 알고리즘

 

위 문제를 밸만 포드 알고리즘으로 풀이한 코드는 다음과 같습니다. 

본 문제에서는 negative cycle이 존재할 가능성이 없기 때문에 해당 부분은 구현하지 않았습니다. 

import heapq
V = int(input())
E = int(input())
from collections import defaultdict
graph = defaultdict(list)
for _ in range(E) :
    s, e, c = [int(x) for x in input().split()]
    graph[s].append((e, c))


start, end = [int(x) for x in input().split()]
distance = {x : float('inf') for x in range(1,V+1)}

def BF(graph, start) :
    distance[start] = 0

    for i in range(len(graph)) :
        for node in graph :
            for neighbor in graph[node] :
                if distance[node] != float('inf') and distance[neighbor[0]] > distance[node] + neighbor[1] :
                    distance[neighbor[0]] = distance[node] + neighbor[1]
    return distance

dists = BF(graph, start)
print(dists[end])

 

하지만 본 풀이는 시간 초과가 떴습니다

 

다시 문제를 보니 directed graph를 전제로 할 필요가 없었고, 또한 negative weight도 전제가 되있지 않기 때문에 다익스트라로 바꾸어 풀었고 문제를 풀 수 있었습니다.

 

[2] 다익스트라 풀이

import heapq
V = int(input())
E = int(input())
from collections import defaultdict
graph = defaultdict(list)
for _ in range(E) :
    s, e, c = [int(x) for x in input().split()]
    graph[s].append((e, c))


start, end = [int(x) for x in input().split()]
distance = {x : float('inf') for x in range(1,V+1)}

def dijkstra(start) :
    priority_q = []
    distance[start] = 0
    heapq.heappush(priority_q, (0,start))

    while priority_q :
        curr_dist, curr_state = heapq.heappop(priority_q)

        if curr_dist > distance[curr_state] :
            continue

        for neighbor in graph[curr_state] :
            cost = neighbor[1] + curr_dist
            if cost < distance[neighbor[0]] :
                distance[neighbor[0]] = cost
                heapq.heappush(priority_q, (distance[neighbor[0]], neighbor[0]))

dijkstra(start)

print(distance[end])