No Limitation
[Reinforcement Learning] Alphago, MCTS 본문
본 포스팅은 노승은 님의 바닥부터 배우는 강화학습 교재를 중심으로 작성되었고 카이스트 산업 및 시스템 공학과 신하용 교수님의 동적계획법과 강화학습 강의 자료를 참고해 작성되었습니다.
이번 포스팅에서는 '강화 학습' 일반 대중에도 주목을 받게 되었던 핵심적인 event인 '알파고 vs 이세돌'에서 사용된 Alphago (original algorithm) 알고리즘에 대해 공부해보겠습니다. 구글 딥마인드에서 개발이 되었던 알고리즘이었고 바둑 대국을 수행하기 위해 고안된 알고리즘이고 큰 파장을 불렀었던 강화학습 기법입니다. 구체적으로 어떻게 동작하였는지 살펴보겠습니다.
알파고를 이해할 때는 크게 "학습(Learning)"과 "실시간 플래닝(Decision-time planning)" 이 2단계를 걸쳐 구성이 됩니다. 학습 단계는 알파고가 이세돌을 만나기 전 훈련을 하는 과정을 의미하는데, 여기서는 사람들이 두었던 play들을 미리 학습을 수행하는 단계와 직접 self-play를 통해 학습을 수행하는 단계로 나뉘어지게 됩니다. 전자는 지도 학습, 후자는 강화 학습으로 볼 수 있겠네요. 그리고 실시간 플래닝은 이제 이세돌을 만나 대결을 치를 때, 어디에 바둑알을 놓을 지, 시뮬레이션을 하는 과정을 의미하고 여기서 사용되는 거시적인 방법론이 바로 Monte Carlo Tree Search (MCTS)입니다. 그럼 각 세부 사항들에 대해 하나씩 살펴보도록 하겠습니다.
학습
학습 단계는 말 그대로 실시간 플래닝, 즉 MCTS를 수행하기 위해 사용되는 재료들을 만드는 과정입니다. 여기서는 4가지의 네트워크를 필요로 하는데, 크게는 3개의 policy network와 1개의 value network를 사용합니다. 하나씩 살표보도록 하겠습니다.
[1] 지도 학습 기반의 정책 네트워크 π_sl
첫 재료로는 π_sl를 살펴보겠습니다. 우선 가정 먼저 수행한 과정은 6단 이상의 기사가 플레이한 판들을 학습을 수행하는 부분입니다. KGS 바둑 서버에서 데이터를 가져왔으며 총 3천 만개의 데이터를 학습했다고 합니다. 데이터는 바둑판의 상태와 해당 상태에서 실제로 바둑알을 둔 곳의 위치의 쌍으로 이루어져 있게 됩니다.
우선 π_sl은 바둑판의 현재 상태 정보 s를 입력으로 받게 되면, 총 19x19의 361개의 바둑 칸들 중 둘 수 있는 곳에 실제로 돌을 내려놓을 확률을 리턴합니다. 즉, 361개의 클래스에 대해 분류를 수행하는 네트워크로 볼 수 있습니다. 예를 들어 (2,3)에 기사가 돌을 내려놓았는데 네트워크는 (2,3)에는 0.4, (3,3)에는 0.5로 확률을 리턴했다면 그만큼 오차가 발생한 것이므로 이 손실 함수를 바탕으로 네트워크를 학습합니다.
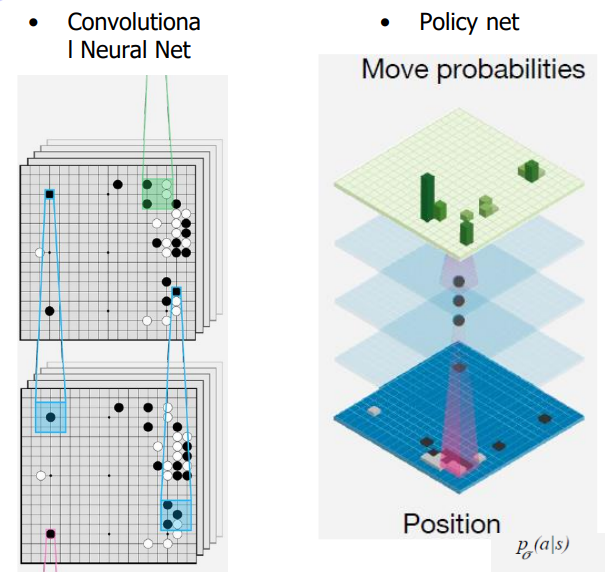
다음과 같이 바둑판의 상태를 입력으로 받게 되는데, 저기서는 이미지 형태를 입력으로 받아 CNN 기반의 네트워크, 즉 컨볼루션 레이어를 사용하여 네트워크를 구축하게 됩니다. 구체적으로는 19x19에 여러 feature를 가지고 있는 정보를 더 넣게 되는데, 예를 들어 흑돌만 있는 판의 경우, 백돌만 있는 판의 경우, 과거 history 등등의 사람의 지식을 이용하여 만든 feature를 총 48겹을 쌓아서 input으로 넣었다고 합니다. 그래서 이미지의 RGB 채널처럼 다양한 feature 정보를 채널 형태로 겹겹이 쌓아서 만들게 됩니다. 그리고 그렇게 입력을 받고, 13개의 컨볼루션 레이어 층을 구축하게 되고, 마지막 레이어에 classify를 위한 FC layer를 두게 됩니다. 즉, 이렇게 3천만 데이터를 학습하고 처음의 결과는 57%의 확률로 정답을 맞히게 됩니다. 저 정확도는 "이 상황에서 사람은 어디다 두었을까?"를 맞히는 확률을 의미합니다.
[2] roll-out 정책 네트워크 π_roll
π_roll는 π_sl의 가벼운 버전입니다. π_roll은 π_sl과 마찬가지로 바둑판의 상태 s를 입력으로 받아서 각 액션의 확률 분포를 리턴하게 됩니다. 크게 다른 점은 없지만 "훨씬 가벼운" 네트워크라는 것이 큰 특징입니다. 이 경우 매우 심플하게 구축이 되는데, π_roll의 경우 하나의 fully connected layer만 존재하게 됩니다. 즉, π_sl에 비해 성능은 훨씬 더 떨어집니다 (24.2%). 하지만 계산 속도가 훨씬 빠르기 때문에 추후 실시간 플래닝 과정에서는 이 π_roll을 이용해서 시뮬레이션을 수행하게 됩니다. 시뮬레이션에 대해서는 뒤에서 자세하게 설명드리도록 하겠습니다.
[3] 강화 학습 정책 네트워크 π_rl
자 이제 열심히 수업을 들었으니 이제 직접 본인이 문제를 풀어봐야겠죠. 바로 이 부분을 수행하는 역할이 바로 π_rl입니다. π_rl은 π_sl과 완벽히 똑같이 생긴 뉴럴 네트워크입니다. 즉 다른 의미로, "π_rl은 π_sl의 가중치로 초기화"하는 것입니다. 바로 이 부분이 핵심입니다. 랜덤으로 초기화 되어있으면 그냥 아무데나 막 바둑 돌을 두었을텐데 학습된 π_sl의 가중치를 사용해서 보다 의미있는 경험들을 잘 쌓을 수 있게 됩니다. 이 π_rl은 π_sl의 경험을 바탕으로 self-play를 수행하게 됩니다. 즉, 자신의 복제본을 열심히 풀에 저장해놓고 (정확히는 history) 그들과 대국을 펼쳐 경험들을 모으는 것입니다. 예를 들어 처음 3시간 정도 학습된 모델을 1차 저장하고 10시간 학습된 모델을 그 다음에 풀에 저장하고 지금 16시간째 플레이 중이라면 바로 이 모델을 이 이전 3시간과 10시간 학습한 모델과 대국을 펼치어 학습을 수행하는 것입니다. 이 π_rl에서는 보상 함수는 이기면 1, 지면 -1로 하였고 그 외의 중간 보상은 전혀 없는 것이 특징입니다. 또한 policy gradient 방법을 사용하였고 REINFORCE 방법을 사용하였습니다. γ는 1을 사용했다고 하네요. 즉 조금 더 강한 실력을 갖는 모형이 완성됩니다. 하지만 이 π_rl은 오히려 실제 경기를 뛰는 녀석이 아닙니다. 오히려 value network을 구하는 데 사용되는 서브 재료입니다.
[4] 밸류 네트워크 v_rl
자, 이제 마지막 재료인 v_rl에 대해 살펴보겠습니다. v_rl의 구조는 π_sl, π_rl과 동일하게 되지만, 아웃풋은 1개의 값을 리턴해야 하기 때문에 마지막 output layer가 상이하게 됩니다. 즉, 이 경우 정확한 의미는 "주어진 상태 s부터 시작해서 π_rl을 이용하여 플레이 했을 때 이길지 여부를 리턴"하는 함수입니다. 즉, 승자를 예측하는 함수가 되는 것입니다. 바로 이 네트워크를 시뮬레이션을 하는데 π_roll과 같이 MCTS에 사용되게 됩니다.

이 4개의 재료에 대해 개략적인 정리를 하면 다음과 같이 나타낼 수 있습니다.
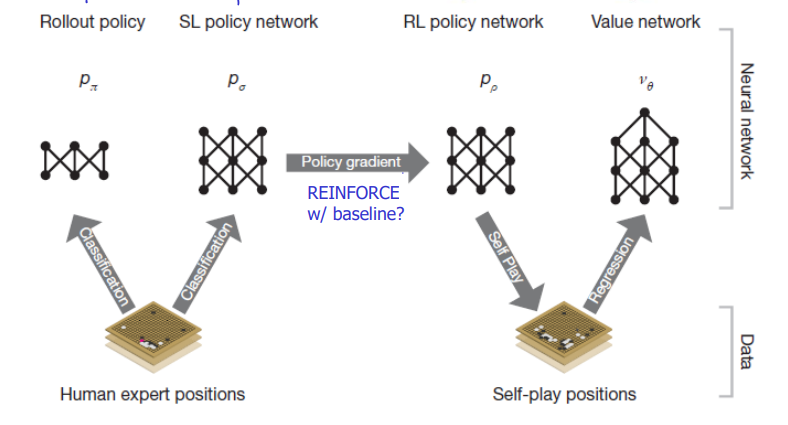
실시간 플래닝
이제 앞서 구축한 4가지 재료를 활용해서 실제로 이세돌과 대결을 펼칠 때 사용되는 MCTS의 방법에 대해 살펴보겠습니다. MCTS는 말 그대로 "많이 둬보는" 단순한 방법입니다. 그래서 tree의 edge는 액션이 되고 node는 상태가 됩니다. 하지만 이 트리의 크기는 바둑의 경우의 수를 생각해보면 기하급수적으로 커지게 됩니다. 바둑의 경우는 10^170 정도의 상태 경우의 수를 갖는다는데 이는 말이 안되는 수치입니다.

그래서 모든 경우를 다 보는 것이 아니라 "어떤 상황에서 그 상황에 특화된 최적 액션을 수많은 시뮬레이션을 빠르게 수행"해서 다음 수를 찾고자 하는 것이 핵심 아이디어입니다. 그리고 이를 수행하기 위해 사용되는 것이 바로 앞선 4가지 재료, π_sl, π_roll, π_rl, v_rl이 됩니다. 조금 더 이해를 쉽게하기 위해 다음 슬라이드를 살펴보겠습니다.
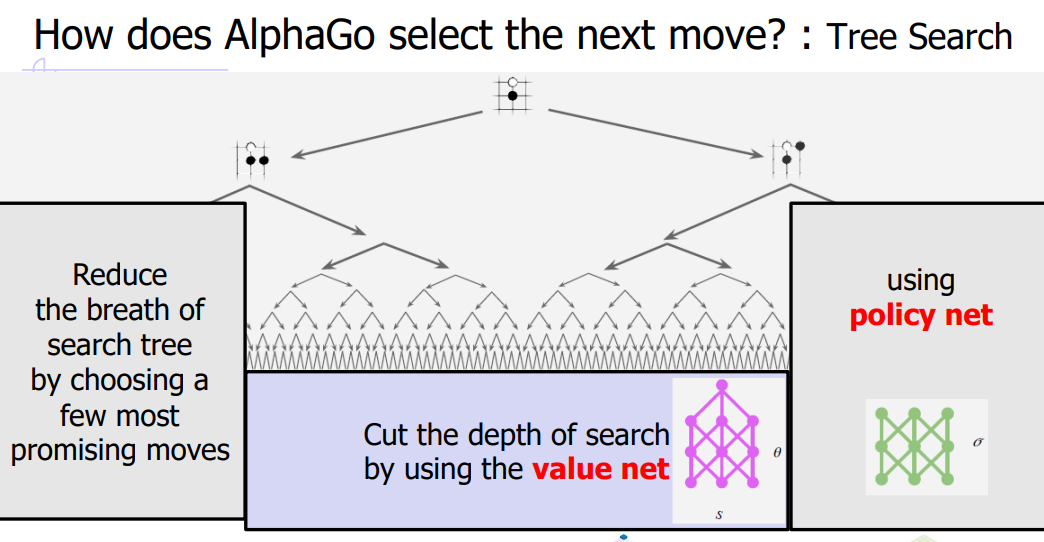
즉, 위와 같이 무수하게 큰 트리에서, 이 트리는 선택의 폭이 넓어, 즉 breath가 크기도 하고 그 깊이가 깊기도 합니다. 바로, 이런 부분해서 policy network가 추천하는 확률이 높은 몇 개의 action에 대해서만 branching을 해보라는 측면에서 트리의 breadth를 줄일 수 있습니다. 반면, 모든 대전이 끝날 때까지의 결과를 바탕으로 value를 계산하지 않고 value network를 사용해서 이 깊이가 깊어지는 문제를 막을 수 있습니다. 그리고 이 기능을 수행하는 것이 바로 앞서 말씀드린 4개의 재료들이 역할을 수행하게 됩니다. 그렇다면 구체적으로 어떻게 MCTS가 이 4개의 재료를 활용하는 지를 공부해보겠습니다.
알파고에서 MCTS는 '선택', '확장', '시뮬레이션', '역전파' 4단계를 거치면서 게임을 수행하고, 한 loop를 수행하면 트리에 노드 한 개가 매달리게 됩니다. 노드는 바둑판의 한 상태가 됩니다.
[1] 선택
'선택'은 루트 노드에서 출발해서 리프 노드까지 도달하는 전 과정을 의미합니다. 예를 들어 아래 사진의 경우 붉은 색 경로를 통해 리프 노드에 도달한 경우를 보여줍니다.

자 그러면 저기서 저 action들이 각각 어떻게 선택이 된 것일까요? 즉 이는, 기존의 학습되어진 네트워크를 활용해서 value를 높게 하는 액션을 선택하게 되는 것입니다. 구체적으로는 아래 수식처럼 수행이 됩니다.

즉, Q+u 값을 가장 크게 하는 action을 선택하게 되는 것입니다. 그리고 시뮬레이션을 진행할수록, 즉 경험이 쌓일 수록 Q(s,a)의 영향력은 커지고, u(s,a)의 영향력은 줄게 됩니다. 그러면 이 Q, u에 대해 디테일한 내용을 살펴보겠습니다.
노승은 님께서 사용하신 예시를 가지고 같이 살펴보겠습니다. ( 개인적으로 정말 정리가 잘 된 것 같습니다. 노승은 님 교재는 꼭 참고하셔서 공부하시길 추천드립니다...! ) Q(s,a)의 의미는 "s에서 a를 선택한 이후 도달한 리프 노드들의 평균"을 통해 계산됩니다. a를 선택한 이후 최종적으로 도달한 리프 노드의 value가 높으면 Q(s,a)가 증가하고, 밸류가 낮으면 감소하게 됩니다. 예를 들어 어떤 상태 s78에 위치했을 때 액션 a33를 선택하는 경험을 100번 했다고 하면, 그 100번을 했을 때 도달하게 되는 리프 노드들을 s_l1, s_l2, ... s_l100이라고 하면 Q(s78, a33)은 다음과 같이 계산될 수 있습니다.

저기서 V(sl)에 대해서 어떻게 계산되는 지는 시뮬레이션에서 자세하게 다루겠습니다. 즉, 저렇게 리프 노드들에서 구해진 value의 평균을 바탕으로 Q를 구하게 됩니다.
다음으로 u는 어떤 과정을 통해 구해지는 지 살펴보겠습니다.

즉, 사전 확률(prior)를 사용하는 것인데요, 시뮬레이션을 해보기 전에 사람이라면 두었을 법한 수에 높은 확률을 부여하는 것입니다. 다만, 이는 그대로 π_sl을 사용하는 것이 아니라 방문 횟수가 높아질수록 그 사전 확률의 영향을 감소시키게 됩니다. 그래서 점차 시뮬레이션을 수행할 수록 Q의 영향은 커지지만 u의 영향이 작아지게 되는 것이죠. 그리고 저기서 π_rl이 아닌 π_sl을 사용한 것은 π_sl이 보다 다양한 액션을 시도하는 정책이기 때문에 π_sl로 초기화를 해주면 더 다양한 경험을 쌓을 수 있다고 합니다. ( 더 exploration이 보장되나 봅니다. )
자 이렇게 이미 학습된 Q와 u를 활용해서 action을 선택해 트리에 추가할 노드를 만들어내는 과정을 '선택'을 통해 수행됩니다.
[2] 확장
노드를 만들었다면 이제, 이 리프노드를 트리에 추가해주는 과정을 필요하게 됩니다. 이 과정에서 필요한 사전 확률부터 N, Q 값들을 초기화해줍니다.


그리고 이 추가된 노드에서도 액션을 선택해서 또 반복하고 ... 이러한 스텝을 진행하게 됩니다.
[3] 시뮬레이션
정식 노드가 추가되고 나서 이 노드의 가치를 평가해주어야 합니다. 이 가치를 계산하는 것은 위의 V(s_l)을 계산해주는 것과 같은 의미입니다. 그럼 이 시뮬레이션은 어떻게 수행해야 할까요? 만약, 노드가 추가할 때마다 시뮬레이션하는 과정이 느리게 되면 프로그램은 엄청난 시간 소모를 하게 될 것입니다. 따라서 '빠르게' 시뮬레이션을 수행하는 무언가가 필요하며 바로 이 과정에서 앞서 배웠던 π_roll을 사용하게 되는 것입니다. 즉, 이 π_roll을 이용하면서 보상 -1, 1을 획득할 때까지 게임을 수행합니다. 그 결과값을 result라고 하겠습니다. 하지만 π_roll 이 녀석의 정확도가 높지 않기 때문에 그러한 부분을 보완하기 위해 v_rl 역시 마찬가지로 도입합니다. 즉, 이 둘의 결과를 반반씩 섞어 사용하는 것이죠. 즉, 아래 그림과 같이 전개됩니다.

실제 논문에서 리프 노드를 평가할 때 둘을 각각만 사용했을 때보다 반반 섞었을 때가 더 좋았다고 합니다.
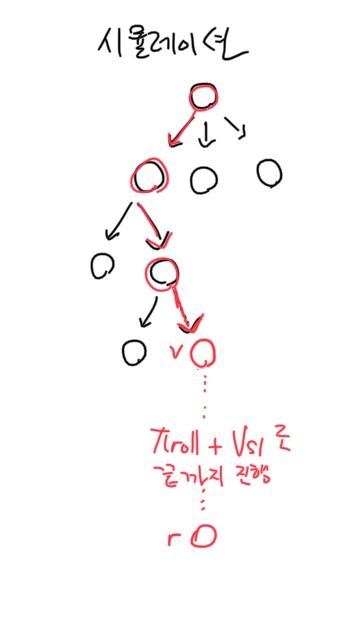
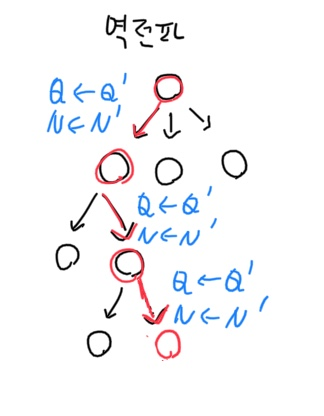
[4] 역전파
사실 일반적으로 딥러닝에서 사용되는 gradient의 의미는 아닙니다. 말 그대로 시뮬레이션을 수행해준 다음에 Q와 N을 업데이트 해주는 과정이 리프 노드에서 다서 '역으로 전파'되어 업데이트가 되기 때문에 역전파라는 용어를 사용합니다. 즉 밑의 수식처럼 업데이트가 되는 것입니다.

지나온 엣지들에 대해 방문 횟수를 1 늘리고, Q에 대해서는 V의 방향으로 업데이트를 수행하였습니다. V가 좋으면 좋은 Q 값을 얻지만 V가 나쁘면 나쁜 Q를 얻게 되는 것입니다. 즉, 이런 과정을 통해 update가 수행되게 됩니다.
자 이런 과정을 통해 지금까지 수행한 것은 바로 "MCTS"를 통해 거대한 트리를 만든 것입니다!! 이를 잊으면 안됩니다. 즉, '선택', '확장', '시뮬레이션', '역전파'는 트리를 하나 만든 것입니다. 그리고 이제 이 트리를 바탕으로 액션을 선택하게 되는 것입니다.
예를 들어 아래 사진을 봅시다.

위 s에서 3개의 액션 a1, a2, a3가 있다고 하면, 이 중에서 어떤 action이 가장 좋은 action이 될까요? MCTS를 구축할 때 사용한 방법대로 Q(s,a)가 가장 큰 action을 고르면 될 것이라고 생각하기는 쉽지만 실제 MCTS 구축 이후 action을 선택할 때는 Q가 아닌 N이 가장 큰 action을 고른다고 합니다. 이 이유는 MCTS를 구축하는 중에 그 엣지가 가장 유망한 엣지였다는 것을 의미하기도 합니다. 또한 '신뢰도'를 같이 고려하는 것입니다. A로 갔을 때 50점을 얻는 사람이 3명있고 B로 갔을 때 45점을 얻은 사람이 3000명 이면 B로 간다는 것이죠. 즉 이러한 메커니즘으로 최종 액션을 선택하게 됩니다.
이상 '알파고'에 대한 개념을 정리해보았습니다. 추후에 기회가 된다면 이의 개선안인 알파고 제로도 정리하도록 하겠습니다.
긴 글 읽어주셔서 감사합니다!




