No Limitation
[Deep Learning] Variational Autoencoder 본문
본 포스팅은 Ian Goodfellow et.al 의 Deep learning 교재와 카이스트 산업 및 시스템 공학과 박찬영 교수님의 지식서비스를 위한 기계학습 강의, NAVER 이활석님의 오토인코더의 모든 것 강의를 참고하여 정리하였습니다.
오토인코더의 모든 것 강의 2
https://www.youtube.com/watch?v=rNh2CrTFpm4
Variational Autoencoder는 기본적으로 "생성 모델"로 간주하게 됩니다. 본 포스팅은 autoencoder에 대한 기본 내용을 이해하는 전제하에 개념을 정리하고자 합니다.
우리가 어떠한 이미지 정보를 가지고 있다고 하면, 그 이미지에는 다양한 feature들, 특성들이 존재하게 됩니다. 예를 들면 머리 색깔, 눈의 크기 등과 같은 정보들이 들어 있겠죠. 이를 잠재적인 정보를 가지고 있는 어떠한 feature를 latent feature라고 표현을 하게 됩니다. 그리고 보통 z로 나타냅니다. 만약 우리가 다음과 같은 확률 분포 P(x,z)를 알게 되면, 어떠한 given feature 하에 우리가 원하는 image를 쉽게 generate할 수 있게 됩니다.

p(x,z)를 베이즈 정리에 의해 우항처럼 나타낼 수 있는데요. p(z)는 말그대로 사전 확률을 의미하고 p(x|z)는 이러한 z하에 x가 갖는 likelihood입니다. 이 수식을 조금 더 autoencoder의 특징 (generator)을 담아 정리하면 다음과 같이 표시할 수 있겠죠.

그리고 저 사전 확률 p(z)는 보통 가우시안 분포를 가정하게 됩니다.
하지만 저 p(z)가 정말 신뢰할 만한 수치일까요? 아래 그림을 살펴보겠습니다.

가우시안 분포를 바탕으로 MLE를 계산하면 MSE를 바탕으로 계산이 이루어지는데 위 (a), (b), (c)에서 의미상으로 보면 사람은 (c)가 (b)보다 더 의미적으로 가깝다는 것을 알 수 있습니다. 왜냐하면 (b)는 2의 앞단이 지워졌기 때문이죠. 반면 (c)는 단지 몇 픽셀 이동만 했을 뿐 (a)랑 크게 다르지 않으니까요. 하지만 모형은 MSE를 바탕으로 MLE를 수행하기 때문에 (b)를 더 좋은 샘플로 간주하게 됩니다. 즉 MSE가 더 작은 이미지가 의미적으로 더 가까운 경우가 아닌 이미지들이 많기 때문에 현실적으로 올바른 확률 값을 가질 수가 없는 것이죠. 즉, 이 경우는 단순히 p(z)에서 샘플링하는 것이 그다지 좋지 못하다는 것을 암시합니다.
그래서 우리는 x 가 given일 때, 좋은 z를 통해서 infer를 하면 좋으니까 결국 p(z|x)를 계산해서 좋은 z를 찾고자 하는 것입니다. 예를 들어 이미지 '2'가 주어지고 p(z|x)를 통해 z를 infer할 수 있으면, 이는 어떤 feature가 2를 generate하는 지를 쉽게 알 수 있음을 의미하게 됩니다. 그리고 이 z를 살짝 바꾸어서 또 다른 2를 만들 수도 있기 때문입니다. 그러면 결국 p(z|x)를 아는 것이 핵심이겠군요.
이는 베이즈 룰에 의해 아래 수식처럼 나타낼 수 있습니다.
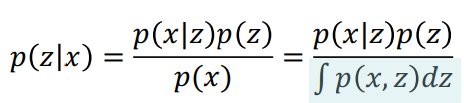
하지만, 위 수식에서 파란색 음영으로 표시된 부분은 z 값을 알 수 없는 상황에서 z에 대한 적분을 구할 수 없게 됩니다. 즉, 직접적으로 p(z|x)를 접근할 수 없는 문제가 발생하죠. 이래서 우리는 이 p(z|x)는 잘 몰라도 이와 근사한 무언가를 이용하면, 구체적으로는 q_∅ (z|x) 을 통해 근사시킬 수 있으면 이 문제를 풀 수 있지 않을까하는 아이디어에 착안한 개념이 바로 변분 추론 (Variational Inference) 입니다.
자 그렇다면, p(z|x)에 근사한 q_∅ (z|x)을 찾는다고 했는데 ∅로 parameterized된 이 ∅를 어떻게 찾을 수 있을까요? 이는 q_∅ (z|x)와 p(z|x)의 유사성을, 분포의 유사성을 바탕으로 minimize를 수행해야 하기 때문에 Kullback-Leibler Divergence (KL Divergence)를 사용하게 됩니다. notation은 아래와 같이 표기가 가능하며 결국 아래 빨간 식을 만족하는 ∅를 찾는 것으로 task가 정의됩니다.
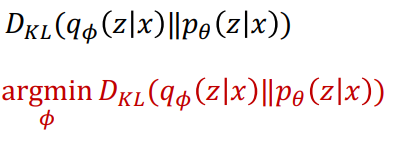
자 그전에 간단하게 KL Divergence (편의상 KL이라고 하겠습니다) 가 정확히 어떤 의미를 갖는지를 살펴볼까요. 우선 KL은 'expectation of the information difference between two probability distributions'라고 정의할 수 있습니다. 즉 정보의 차이라고 볼 수 있는데요. KL에서는 이 정보라는 것은 사건이 발생할 확률이 많은 경우에 그 정보를 담고 있는 양이 적다는 가정을 기저에 깔게 됩니다. 즉, 이미 사람들이 많이 알고 있는 사건이라면, 즉 P(x)가 크다면, 여기서 얻어지는 정보의 양은 크지 않다는 것이죠. 따라서 logP(x)가 주어지면 information은 log(1/P(x))로 나타낼 수 있고 이것이 바로 Information이 됩니다.
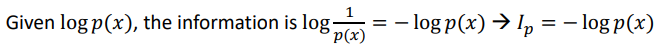
그리고 p, q에서의 information 차이를 계산할 수 있게 되고, 그 expectation의 형태가 바로 KL이 됩니다.
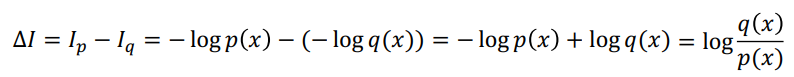
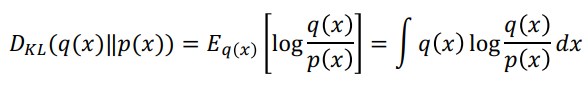
자 이 KL은 중요한 특징이 있는데요. 첫번째는 교환 법칙이 성립하지 않는다는 점입니다. 즉 아래 그림과 같이 P와 Q의 위치가 바뀌면 그 값이 달라진다는 것입니다.
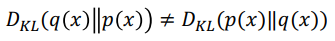
또한 Non-negative하다는 특징이 있습니다. 이 특징은 뒤에서 매우 중요하기 때문에 꼭 기억하시기 바랍니다. 본 포스팅에서는 증명 과정을 따로 다루지는 않겠습니다.
그렇다면 다시 본론으로 돌아와서 우리는 P(z|x)를 추론하기 위해 다음과 같은 objective function을 얻었습니다.
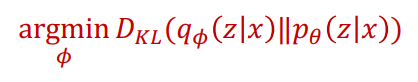
그렇다면 저 부분을 optimize하기 위해 우선 KL 수식부터 풀어써보면 다음과 같이 전개가 됩니다.

즉 이를 조금 더 깔끔하게 정리해보면
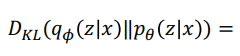
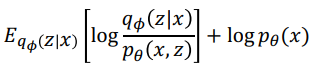
다음과 같이 전개가 됨을 확인할 수 있습니다. 이 수식을 전개하는 것은 단순하게 log를 푸는 것과 베이즈 룰을 사용하면 금방 전개할 수 있습니다.
자 그럼 이 수식을 가지고 ∅에 대해 optimize를 해야하는데, p(x) term이 있기 때문에 여전히 계산을 바로 할 수 없게 됩니다.
자 해당 logp(x)는 어떻게 전개할 수 있을까요? 위 수식을 logp(x)에 대한 수식으로 풀어서 정리해보겠습니다.
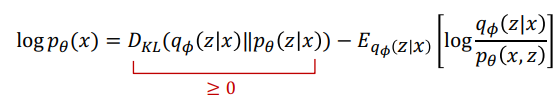
자 다음과 같이 전개가 되는데 여기서 KL의 경우 non-negative하다는 것을 앞에서 살펴보았으므로 이는 결국 다음과 같은 lower bound를 가지게 됩니다.

즉 KL=0이라고 하는 것보다는 좌항이 더 크게 되겠죠. 이 수식을 더 정갈하게 정리하면 결국 우항과 같은 수식이 나오고 이 L(θ, ∅, x)이 결국 Lower Bound가 됩니다. 이는 logP(x)에 대한 lower bound이므로 'Evidence Lower Bound(ELBO)'라고 표시할 수 있습니다.
Evidence에 대해 혹시라도 낯선 분들이 계실까봐 다음 notation을 간단하게 정리해보겠습니다.
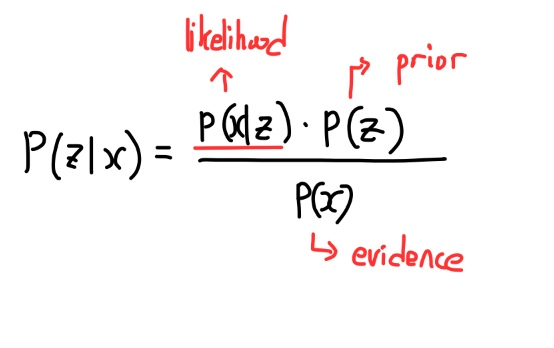
이는 간단한 정의(?) 같은 개념이니까 참고하시면 좋을 거 같습니다. 위처럼 P(x)를 기본적으로 evidence로 표시를 하기 때문에 logP(x)에 대한 lower bound이기 때문에 ELBO라고 명명한 것입니다.
자 그러면, 우리는 KL에 대한 식으로 정리하면 다음과 같이 rearrange를 할 수 있습니다.
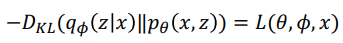
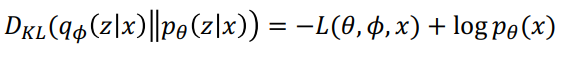
위 수식을 보면 Lower bound과 logP(x)에 대한 수식으로 전개되는데 우리는 이 수식을 ∅에 대해 optimize를 할 건데, logP(x)는 ∅와 무관한 수식이 됩니다. 따라서 우리의 task는 KL을 minimize하는 task에서 Lower bound를 maximize하는 task로 바뀌게 됩니다.
자 이 의미는 수식을 다음과 같이 정리해서 그림과 같이 설명을 해보겠습니다.
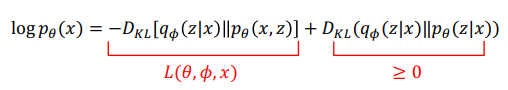
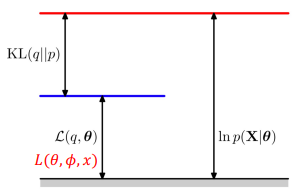
logP(x)에 대한 수식으로 바꾸게 되면 이는 아래 그림과 같이 나타내는데 고정된 logP(x)에 대하여 KL을 minimize한다는 것은, 곧 아래에 있는 L(θ, ∅, x)을 maximize하는 것과 동일한 의미가 됩니다.
그러면 이 L(θ, ∅, x)를 maximization을 해주어야 하기 때문에 mini batch B만큼을 뽑아 gradient를 계산해주어야 하므로 수식을 전개해보면 다음과 같이 나옴을 알 수 있습니다.

하지만 우측 끝단 수식을 보면 expectation을 구하는 수식에 여전히 z값을 내포하고 있으므로 저 식을 바탕으로 gradient를 수행하기에는 무리가 있어 보이죠. 따라서 우리는 저 expectation을 구하는 데에 integral이 아닌 monte carlo방법으로 sampling을 해서 수행하면 어떨까하는 아이디어가 나왔고 이를 이용해서 expectation을 구할 수 있게 됩니다. 이는 아래 수식처럼 전개가 됩니다.
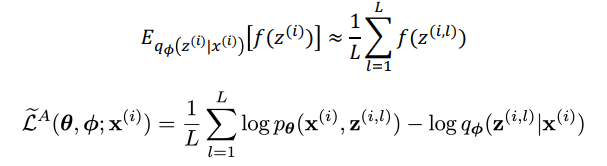
샘플 L개를 뽑게 되고 그 샘플들에 대한 Monter carlo 평균을 구하게 되면 아래 L_A와 같이 loss function이 정의가 되게 됩니다. 하지만 q에서 뽑는 L개의 샘플에 대해서 값을 구하기 때문에 MC 방법에서 나오는 공통적인 한계점인 'high variance'를 갖는다는 한계점을 가지게 됩니다. ( 여기서 L은 보통 작은 수를 사용하는데 심지어 1을 사용할 수도 있다고 합니다. )
자 우선, 이 문제를 다루기 전에 앞에서 정리한 ELBO 의 구조를 다시 찬찬히 뜯어보도록 하죠.

개인적으로 교수님께서 굉장히 잘 정리하신 슬라이드라는 생각이 듭니다. 복잡한 내용이 심플한 한 슬라이드로 정리가 되어 있습니다. 우선 L(θ, ∅, x)을 정리해보면 다음 아래와 같은 2개의 term으로 구성이 되며, L(θ, ∅, x)를 maxmimize한다는 것은 결국 아래의 수식을 각각 minimize, maximize를 하게 됨과 동일한 의미를 가지게 됩니다. 처음 왼쪽 항은, q_∅ (z|x)항과 p_θ (z)항의 KL을 minimize, 즉 거의 근사시킨다는 것을 의미하게 됩니다. q_∅ (z|x)는 사후 확률이고 p(z)는 사전 확률이기 때문에 사후 확률은 사전 확률에 근사시킨다는 것을 의미하겠네요. 그리고 앞서 말씀드렸듯, 사전 확률 p(z)는 일반적으로 가우시안을 사용하게 됩니다. 그리고 뒤에서 언급드리겠지만, Variational Autoencoder에서는 기본적으로 가우시안 기반에서 사용이 가능한 한계점을 가지게 됩니다. 그 부분에 대해서는 뒤에서 자세하게 설명드리도록 하겠습니다. 또한 우측 항의 경우는 재구성의 퀄리티를 의미한다고 되어 있는데, 즉 q_∅ (z|x)에서 샘플링한 z가 실제로 x를 잘 구축한 경우에는 해당 값이 커지겠죠. 즉, 이 구조가 바로 autoencoder의 구조를 반영하게 됩니다. q_∅ (z|x)는 encoder 부분을 담당하게 되고 p(x|z)가 latent feature z를 바탕으로 new x를 generate하게 되니까요. 이에 대해서도 뒤에서 자세하게 다루도록 하겠습니다.
왼쪽 term은 p(z)를 가우시안으로 가정하기 때문에 가우시안 분포를 입력으로 넣어 계산하면 수식을 구할 수 있고, 우측 수식이 결국 monte carlo를 통해 expectation을 구하게 됩니다. 이는 다시 정리하면 다음과 같이 전개가 됩니다.
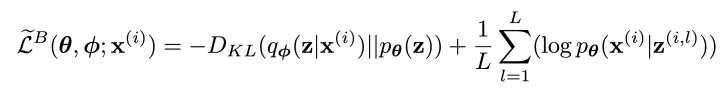
오른쪽 term이 기존 expectation form에서 monte carlo 형태로 바뀐 것을 확인할 수 있습니다. 그리고 이렇게 전개가 되면 더 이전 monte carlo수식보다 더 분산이 준다고 하네요. ( 이 부분은 저도 명확히 이해는 못했습니다 ㅠ )
위 왼쪽 regularization term을 가우시안을 사용하게 되면, 다음과 같이 수식이 전개됩니다.

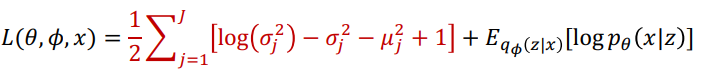
이 부분에 대한 증명 과정은 따로 본 포스팅에서는 추가하지 않겠습니다.
자 그렇다면 다시, 우리는 계속 ∅에 대해 어떻게 objective function을 optimize할 것인지에 대한 숙제를 풀어가고 있습니다. 위 수식에서 결국 regularization term은 가우시안 분포를 넣어서 계산할 수 있다면 결국 우측에 있는 reconstruction quality 부분을 어떻게 optimize할 것인지가 숙제가 되겠네요.
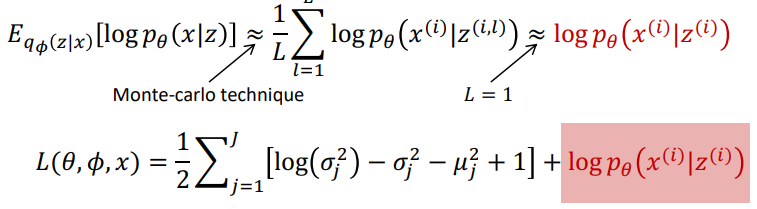
L을 1로 사용했을 경우, 위 expectation 값은 simple한 logp(x|z)가 되고 이 logp(x|z)는 어떠한 분포를 띄냐에 따라 다르게 계산이 이루어집니다. 보통 베르누이 분포나 가우시안 분포를 가정하고 식이 전개가 됩니다. 그리고 여기서, 베르누이 분포를 따른다고 하면 해당 term의 값은 cross entropy 형태가 나오게 되고 가우시안 분포를 따른다고 하면 squared error 형태가 나오게 됩니다.
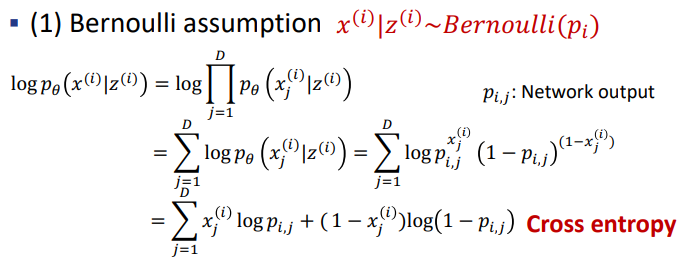

자, 이렇게 되면 이제 L(θ, ∅, x)을 maximize하는 ∅을 찾아 q_∅ (z|x)를 통해 z를 뽑으면 문제가 해결되니까 이제 모든 문제를 풀 수 있을까요? 여기서 안타깝게도 저 방법만 그대로 사용하게 되면 ∅를 구하기 위한 backpropagation을 하는 과정에서 제대로 train이 이루어지지 못하는 문제가 발생합니다. 즉, 이는 바로 p(x|z)에서 random sampling을 통해 계산이 수행되는데 이로 인해 바로 저 loss 즉,
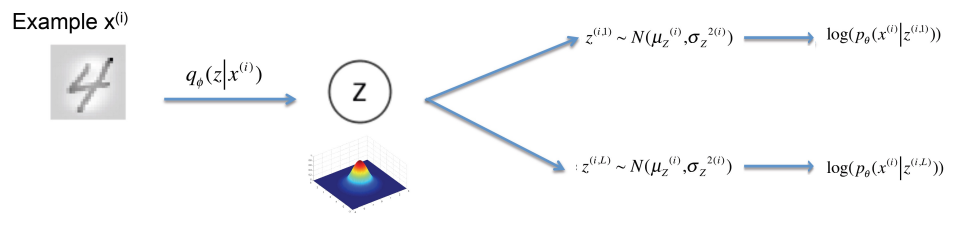
z에서 샘플되어지는 값을 바탕으로 계산되는 logp(x|z)가 미분이 되지 않는 문제가 발생하는 것입니다. 따라서 이 문제를 방지하기 위해, reparameterization trick을 통해 이 문제를 극복합니다.
즉, 기존에는 다음과 같이 샘플들을 뽑아 구해진 z를 사용했는데 그게 아니라, z를 도출하는 mu와 sigma를 ∅을 파라미터로 활용하는 네트워크를 구축하면, 그리고 이들을 활용해서 z를 구하면, 미분이 가능하지 않겠느냐는 아이디어로 이 문제를 해결합니다. 즉, 아래 수식을 보시죠.
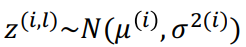
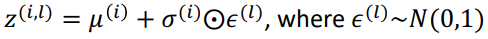
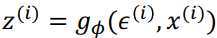
즉 위의 수식이 기존에 샘플링을 통해 z를 구한 것이라면 이를 아래와 같이 mu와 가우시안 분포에서 샘플링된 입실론을 sigma의 element wise 곱을 통해 계산된 값을 z로 사용하면 안되냐는 것입니다. 이를 보다 더 직관적으로 나타낸 것이 아래 그림입니다.
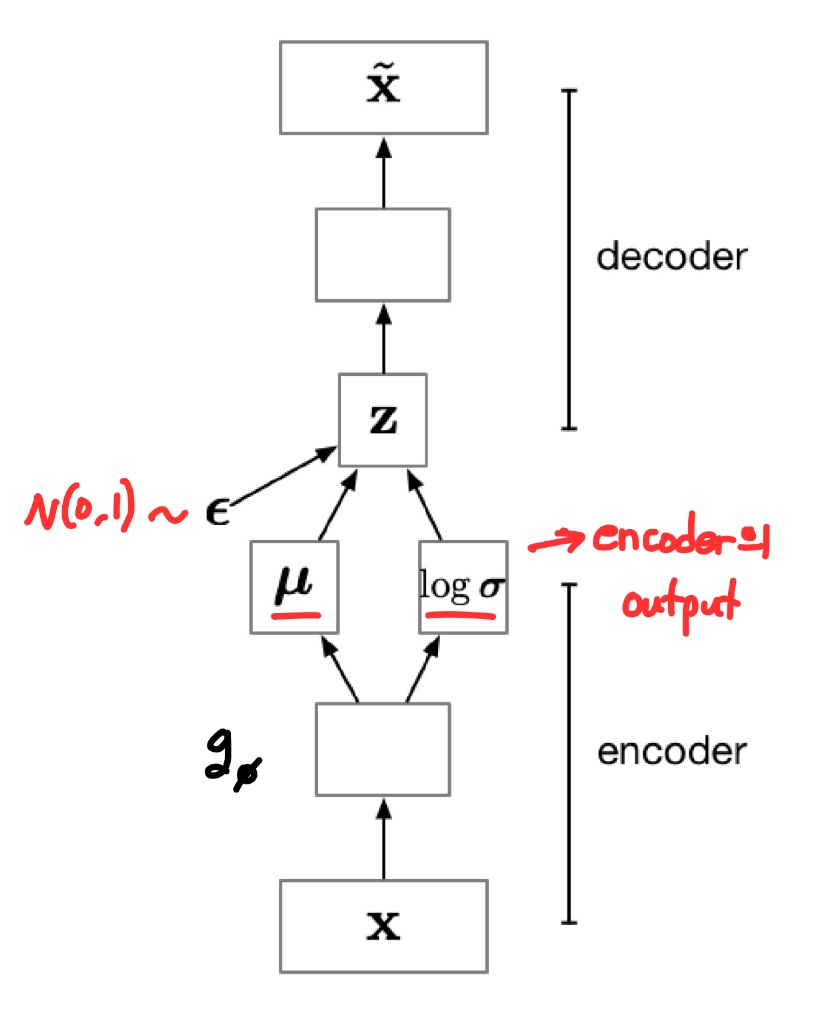
즉, 입력 x가 들어올 때 encoder인 g_∅을 통해 도출되는 mu와 sigma를 가우시안 분포에서 추출한 입실론과의 합을 통해 z를 도출하는 방법입니다. 이를 통해 z는 이전에 샘플링한 것과 동일한 분포를 가지게 되며 동시에 backpropagation을 수행할 수 있게 됩니다.
따라서 최종적으로 구축되는 VAE는 다음과 같은 구조를 가집니다.

이를 간단하게 요약하면,
1. x를 잘 만드는 generator를 학습하고 싶다.
2. 하지만 prior에서 샘플링하니까 잘 안된다.
3. 따라서 이상적인 샘플링 함수에서 샘플링을 하고 싶다.
4. 이상적인 샘플링 함수는 x를 evidence로 주고 그 x에 대해서는 잘 generation되게 하는 z를 샘플링할 수 있는 q_∅ (z|x)를 도입해보자.
5. 이 q_∅ (z|x)를 찾는다는 것은 ∅에 대해 Objective function을 optimize한 ∅를 찾는 것이다.
이렇게 정의할 수 있게 됩니다.
코드도 특별히 살펴보겠습니다. p(x|z)가 베르누이 분포를 따른다는 것을 가정하겠습니다.
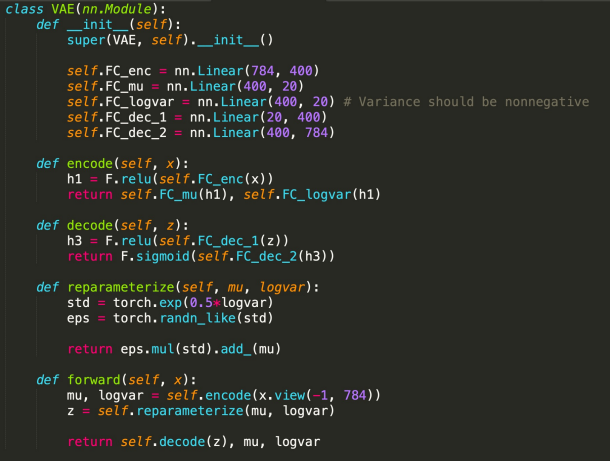
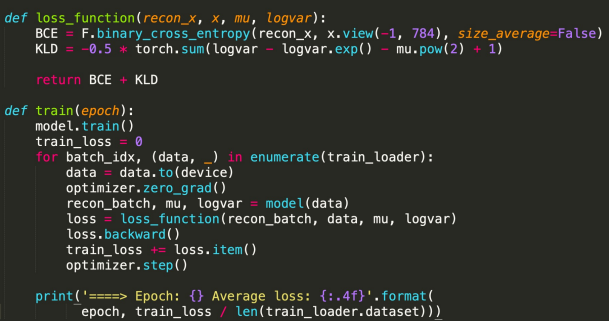
첫 번째 forward 함수에서 encode를 수행한 결과로 도출되는 것이 바로 mu와 logvar임을 알 수 있습니다. 그리고 이를 reparameterize함수로 넘기면 바로 그제서야 z가 도출되게 됩니다. 그리고 학습을 수행하는 과정에서 loss function은 reconstruct quality를 구축하는 cross entropy 부분과 regularized 부분을 구성하는 KL divergence로 계산이 됨을 추가로 확인할 수 있었습니다. p(z)는 가우시안 분포를 가정하기 때문에 가우시안을 넣었을 때의 KL 값을 사용하였습니다. 위에서 언급했듯, VAE는 가우시안 분포일 때 KL을 구할 수 있으므로 이 경우에 주로 사용이 되는데 사실 가우시안을 따르지 않는 경우도 존재하기 때문에 이 부분이 바로 한계점이었습니다. 이 문제를 극복하려고 GAN Loss를 바탕으로 generation을 수행하는 Adversarial autoencoder의 개념이 등장하기도 하였습니다.
여기까지 Variational Autoencoder에 대한 내용이었습니다! 긴 글 읽어주셔서 감사합니다!
'ML & DL & RL' 카테고리의 다른 글
| [Deep Learning] GAN (2) - Evaulating & Various Architecture (0) | 2022.05.30 |
|---|---|
| [Deep learning] Generative Adversarial Networks (1) - GAN Intro, Wasserstein GAN (0) | 2022.05.19 |
| [Deep Learning] Gradient Exploding Debugging 맨 땅에 헤딩하기 (3) | 2022.04.20 |
| [Deep Learning] Basic Algorithms for Gradient-based Optimization (0) | 2022.04.18 |
| [Pytorch] Torchtext 튜토리얼 - '영어' (0) | 2022.03.04 |




