No Limitation
[Reinforcement Learning] Multi-Arm Bandit (2) - UCB1, Bayesian UCB, Thomson sampling 본문
[Reinforcement Learning] Multi-Arm Bandit (2) - UCB1, Bayesian UCB, Thomson sampling
yesungcho 2022. 6. 3. 16:40본 포스팅은 카이스트 산업 및 시스템 공학과 신하용 교수님의 동적계획법과 강화학습 강의 자료를 바탕으로 작성되었음을 밝힙니다.
MAB에 대한 기초 설명이 필요하신 분들은 앞서 작성된 포스팅을 참고하시면 감사하겠습니다!
[Reinforcement Learning] Multi-Arm Bandit (1) - Intro
본 포스팅은 카이스트 산업 및 시스템 공학과 신하용 교수님의 동적계획법과 강화학습 강의 자료를 바탕으로 작성되었음을 밝힙니다. Exploration vs Exploitation 이 둘 간의 어떤 것을 선택하는 지가
yscho.tistory.com
MAB에서 sub-linear regret을 달성할 수 있는 방법 중 하나인 UCB를 지난 포스팅에서 소개해드렸습니다!
그럼 이제 구체적으로 그 UCB가 어떻게 regret을 도출하게 되는 지 알고리즘을 살펴보겠습니다.
이번 포스팅에서 다루게 되는 UCB 알고리즘은 크게 2개인데, 바로 UCB1과 Bayesian UCB입니다!
그럼 UCB1부터 살펴보겠습니다.
UCB1
UCB1을 공부하기 전 concentration inequality 중 하나인 'Hoeffding's inequality'에 대해 잠깐 공부해봅시다. 저도 확률, 통계를 깊게 공부한 게 아니라 수업에서 배울 때도 이해가 안되서 이것 저것 찾아보면서 공부했는데 최대한 제가 이해한 선에서 정리해보겠습니다. 만일 정보가 틀리거나 이상한 부분이 있으면 댓글 남겨주시면 감사하겠습니다!
호에프딩 부등식은, independent하고 identically distribution인 0과 1사이의 확률 변수 X1~Xn이 있을 때, 이들의 표본 평균 Xn_bar가 있다고 해봅시다. 그러면 True mean E[X]가 표본 평균에 u를 더한 것보다 클 확률은 위 사진의 우변보다 작다는 것입니다. 즉 upper bound를 갖는다는 것입니다. 즉, 위 부등식에서 u가 커지게 되면, 저 P는 0으로 수렴하게 되겠죠. 또한 Xn_bar를 구하기 위해 사용된 n이 커질 수록 Xn이 true mean에 가까워지기 때문에 P가 0으로 수렴하게 됩니다.
뭐 저런게 있다는데 그러면, 저게 어떻게 UCB랑 관련이 있다는 건지가 우리에게 중요한 것이죠. 위 수식에 있는 notation들이 UCB에서는 다음과 같이 적용될 수 있습니다. 아래 수식을 살펴보겠습니다. 
E[X]는 true value기 때문에 q(a)로, X_bar는 estimation이기 때문에 Q(a), u는 uncertainty로 볼 수 있기 때문에 U(a)로 볼 수 있습니다. 저 부등식의 성질을 만족하게 때문에 2번째 줄처럼 바꾸어서 표현할 수 있게 되는 것이죠. 그리고 그것이 확률 pt로 주게 되면 3번째 줄처럼 equation을 정의할 수 있고, 이는 U(a)에 대해 정리하면 logarithm 형태의 수식으로 전개됨을 확인할 수 있습니다. 그리고 만일 pt를 t에 따라 감소하는 함수 t^(-4)의 함수로 정의해서 넣게 되면 4번째 줄의 수식처럼 전개가 될 것이고 t와 N(a)에 대한 수식으로 전개됨을 확인할 수 있습니다. 여기서 왜 t에 대해 감소하는 함수를 넣었을까요? t가 증가하게 되면 시간이 지남에 따라 시행 횟수 n이 증가하겠죠. 그러면 위의 호에프딩 부등식처럼 n이 증가함에 따라 p는 점차 감소하는 것을 배웠습니다. 바로 그렇기에 t에 대해 감소하는 지수 함수를 넣을 수 있는 것이죠. 자세한 증명 과정을 본 포스팅에서는 추가하진 않겠지만 t^(-4)에서 -4가 아니라 어떠한 음수 상수를 넣어도 전부 logarithmic을 만족한다고 하네요 ( 증명 과정은 너무 어려워서 별도로 추가하진 않았습니다..ㅠ ). 그럼에도 특별히 (-4)를 선택한 이유는 이를 t^(-4)로 잡았을 때 UCB가 Lai-Robbins regret lower bound를 만족할 수 있다고 합니다 (증명과정에서 필요하기 때문에 (-4)를 사용했다고 하네요.) 따라서 U(a)는 다음과 같이 표기가 될 수 있습니다.

위 수식의 의미를 조금 해석해보면, 만약 우리가 한 slot machine에서 여러번 횟수를 시도하게 되면 그 머신에 대한 uncertainty는 감소하게 되겠죠. 시도를 많이 해보았으니까요. 이게 분모항이 의미하는 바입니다. 반면, 시간이 지남에도 계속 사용하지 않는 slot machine에 대해서는 여전히 uncertainty가 높겠죠. 이러한 머신에 대해서는 uncertainty를 크게 주어 더 exploration을 수행하게끔 만드는 것입니다. 그것이 분자가 의미하는 바입니다.
그럼 우리가 호에프딩 부등식을 이용해서 U(a)를 구했으니 다시 UCB에서 action을 선택하게 되는 goal은 다음과 같이 표기될 수 있습니다.

그냥 Q(a)를 argmax하는 a가 아니라, 저 uncertainty가 추가되는 것이죠. 그리고 이를 바탕으로 total regret을 구하게 되면, sub-linear를 만족하는 것이 나온다고 하네요.
결국 이 UCB는 실제 관측한 reward를 모름에도 Optimism in the face of uncertainty Principle 원칙에 의해 가장 낙관적인 선택을 하게 되면 결국, 이 sub-linear가 만족을 하게 된다는 점이 참 신기한 특징인 것 같습니다. 왜 그렇게 성립이 될 수 있을까요? 바로 초기 호에프딩 부등식에서 가정한 0~1사이에서 reward distribution이 정의된다는 점 때문입니다. 즉 이 가정으로 reward가 늘 저 범위 내에 있기 때문에 UCB가 이러한 조건을 만족하게 되는 것입니다.

만일 reward distribution이 베르누이를 따른다고 하면 저 bound 조건을 만족하게 되겠네요. 하지만 꼭 베르누이처럼 저 bound로 설정이 되있지 않더라도 무조건 UCB가 기능하지 않는 것은 아닙니다. 임의의 lower, upper bound를 설정하게 되고 쉽게 modify해서 UCB가 sub-linear를 만족하게끔 사용이 가능하다고 하네요.

그러면 아예 bound되어 있지 않다면 어떻게 될까요? 예를 들어 gaussian distribution을 따른다고 해봅시다. 그런 경우는 UCB1-Normal이라고 하는 이름을 붙이는 알고리즘으로 사용되는데 아래 수식처럼 U(a)가 정의가 된다고 합니다. 물론 이도 여전히 sub-linear를 만족하구요.

자세한 증명사항은 너무 TMI라서 포스팅에 넣진 않겠습니다. 대강 컨셉만 말씀드리면 호에프딩 부등식에서 가우시안 분포인 경우로 부등식을 modify하게 되면 아래 그림과 같이 식이 전개가 되게 됩니다.

바로 여기서 똑같이 MAB 컨셉들의 항목으로 대입해주면 위처럼 U(a)가 정의되게 되는 것이지요. 그리고 심지어 저 bound되어 있지 않는 distribution이 normal이지 않더라도, 우리는 CLT에 의해 결국 충분히 많이 수행을 하게 되면 저 UCB-normal을 사용할 수 있는 것은 알려져 있다고 하네요.
자 그렇다면 다음으로 Bayesian UCB를 살펴보겠습니다.
Bayesian UCB
일반적으로 베르누이 분포를 따르는 상황에서의 setting부터 살펴보겠습니다. 일반적인 Frequentist setting에서는 비교적 단순하게 Q(a)를 구할 수 있게 됩니다.

자 이 경우는 r(a)가 나오는 수식이 q(a)의 확률에 따라 1 아니면 0의 reward를 갖는 형태, 즉 베르누이를 따르는 형태로 보상이 결정이 됩니다. 그러면 그렇게 나오는 reward들이 있으면 Q(a)는 그들의 단순 평균을 사용하게 되고, 이것을 바로 q(a)에 대한 estimation으로 사용하게 되는 것입니다. 이를 간단하게 표현하면 다음과 같이 나타낼 수 있겠네요.

반면 베이지안 세팅에서는 Q(a)를 하나의 random variable로 보게됩니다. 그래서 이 Q(a)가 갖는 사전 확률 분포( prior distribution )를 정의하고 이에 observation을 통해 얻어지는 reward를 바탕으로 사후 확률 분포 ( posterior distribution )을 구해가면서 점점 Q(a)를 업데이트하는 방법으로 Q(a)를 구하는 방법이 바로 bayesian UCB 방법입니다. 그리고 reward는 바로 저 분포를 따르게 되겠죠. 수식을 보면 history ht가 condition에 들어가 있음을 확인할 수 있습니다.

베르누이 분포에서의 상황에서는 다음과 같이 bayesian UCB를 구할 수 있습니다. 구체적인 흐름을 아래 그림을 통해 따라가보겠습니다.

초기에는 Q(a)는 α0, β0로 베타 분포를 따르는 사전 확률을 정의합니다. 그리고 action으로 r1을 얻게 되면 이를 통해 α, β를 업데이트해서 새로운 사후 확률을 구합니다. 그리고 다시 r2를 얻어 업데이트하고 ... 이를 반복해서 얻게 되면 위의 파란색과 빨간색으로 표시된 것처럼 최종 사후 확률 분포를 구할 수 있고 이렇게 Q(a)를 구하게 됩니다. 추측이긴 한데 베타 분포를 사전 확률로 취한 이유는 베르누이 상황을 만족시키기 위해, 즉, r이 0이면 β업데이트, 1이면 α업데이트를 하는 식으로 업데이트를 해주는 것이 베르누이 상황을 만족하기 때문에 그런 것으로 추측이 되네요.
그렇다면 가우시안 분포 상황에서는 어떨까요? Frequentist setting에서는 우리가 흔히 알듯이 다음과 같이 표기할 수 있습니다.
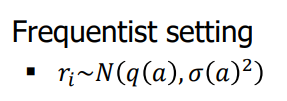

ri가 normal distribution을 따르게 되면 흔히들 알듯, q(a)는 표본 평균을 통해 Q(a)를 추정치로 구할 수 있고 분산 역시 표본 분산을 활용해 구할 수 있게 되죠. 그러면 Bayesian setting에서는 어떠할까요? 마찬가지로 사전확률과 사후확률의 개념을 사용하게 되는데요. 다음과 같은 식으로 업데이트가 되게 됩니다.

그렇다면 이렇게 주어지는 상황에서 어떻게 upper confidence를 구할 수 있게 될까요? 가우시안인 경우를 다시 정리해봅시다.

즉, 이렇게 사후 확률로 Q(a)가 주어지게 되면, 저기서 도출되는 μ와 σ를 활용해서 upper confidence bound을 구할 수 있게 됩니다. 아래 수식이 바로 이를 의미합니다.

이렇게 UCB를 구하는 것이 바로 Bayesian UCB입니다.
다음으로 Thompson sampling으로 넘어가봅시다.
Thompson Sampling
다음과 같은 문제 set을 생각해봅시다.

기존 UCB 같은 경우는 낙관적인 선택에 따라 1의 arm을 당겼을 거지만, Probability matching의 관점에서는 그냥 그렇게 하지 말고 stochastic policy관점에서 생각해보자고 주장합니다. 이게 무슨 소리일까요? 즉 '확률'을 고려하자는 겁니다. 예를 들어,
1을 선택할 거면 그냥 선택이 아니라, P[Q(1) > Q(2)] 확률에 따라 1을 선택하라는 것입니다. 이것이 바로 stochastic policy가 되고 MAB 상황에서는 다음과 같이 수식이 전개될 수 있습니다.

하지만 여기서 문제는 저 probability를 구하는 것이 매우 어렵다는 단점이 존재하게 됩니다.
이 때 이 확률을 매우 쉽게 구하는 방법이 바로 'Thompson sampling'입니다.
Thompson sampling은 쉽게 말해, 사후 확률에서 뽑은 샘플을 사용하라는 것인데, 단순히 이 샘플들만 사용해도 놀랍게도 Lai-Robbins lower bound를 만족한다는 것입니다. 구체적으로 아래 그림을 보시죠.


위와 같은 사후 확률 분포에서, 모든 arm에 대한 샘플을 뽑고 그 샘플들 중 가장 큰 Q(a)를 갖는 arm을 선택하라는 것입니다. 그리고 그렇게 또 Q(a)가 업데이트 되는 방법으로 굉장히 simple하게 접근을 합니다. 저렇게 뽑음으로써 logarithmic이 보장된다고 하네요.
그러면 여기서 궁금한 게, 왜 샘플을 1개씩만 뽑을까요? 충분히 많이 뽑으면 더 좋지 않을까요? 충분히 많이 뽑은 다음에 그 친구들의 평균을 각각 구해서 그 평균 값이 가장 큰 샘플을 뽑는게 더 general하지 않을까 싶습니다. 하지만 아쉽게도 샘플을 많이 뽑게되면 문제가 발생하게 됩니다. 아래 그림을 보시죠.

즉 posterior에서 k개만큼 뽑은 샘플들의 평균을 활용한다고 하면, 아래 2번째 줄과 같이 분포가 바뀌게 됩니다. 샘플 분포로 말이죠. 이 경우 분산은 작아지게 되는데 이 값은 기존 real posterior distribution과 상이해질 뿐더러 이 k가 점점 더 커지게 되면 분산이 점점 더 작아지면서 exploration은 점차 수행을 안하게 되고 결국 분산이 0이 되면 greedy policy와 동일한 형태가 됩니다. 이런 경우 linear regret이 되지 않으므로 sub-linear를 만족하지 못하게 됩니다.
이상 sub-linear regret을 만족시킬 수 있는 MAE 알고리즘으로 UCB1, Bayesian UCB 그리고 Thompson sampling을 살펴보았습니다! 긴 글 읽어주셔서 감사합니다.




